An Intro to the Dot Product

The dot product is so fundamental to linear algebra that it’s easy to take for granted that it works. Here we take a quick look at some of it’s potential by showing how it can be used to calculate the angle between two vectors.

We’re going to show why \(\vec{x} \cdot \vec{y} = \cos{\theta}\lVert \vec{x} \rVert \lVert \vec{y} \rVert \). Our proof will be easier than the one that (as of the time of writing) is given on Wikipedia. It will also be more direct. We’ll do this by considering a few separate cases. Before we get started we’ll mention that the vectors we’re dealing with live in \(\mathbb{R}^n\), which means that \(\vec{x}\) is an \(n-tuple\) (or array) of real numbers. We’ll denote the \(i-th\) component of \(\vec{x}\) as \(x_i\). The dot product of \(\vec{x}\) and \(\vec{y}\) (written \(\vec{x} \cdot \vec{y}\) ) \(:= \sum\limits_{i=1}^{n} {x_i y_i}\). Recall (or prove, if you don’t remember) that

$$ \begin{align} &\sqrt{ \vec{x} \cdot \vec{x} } &&= \lVert \vec{x} \rVert \geq 0 \tag{1}\label{1} \\ &\vec{x} \cdot \vec{y} &&= \vec{y} \cdot \vec{x} \tag{2}\label{2} \\ &(\alpha \vec{ x}) \cdot \vec{y} &&= \alpha ( \vec{x} \cdot \vec{y} ), \text{ where } \alpha \in \mathbb{R} \tag{3}\label{3} \\ \end{align} $$

From (1) and (3) we get}

$$ \lVert \alpha \vec{x} \rVert = | \alpha | \lVert \vec{x} \rVert \tag{4}\label{4} $$

Finally, we notice that the dot product distributes \[ \vec{x} \cdot ( \vec{y} + \vec{z} ) = (\vec{x} \cdot \vec{y}) + (\vec{x} \cdot \vec{z}) \tag{5}\label{5} \]

Hopefully that was all review. Now let’s consider case (a), the simplest case, where \( \vec{y} = \alpha \vec{x} \) for some \( \alpha > 0 \). In this case \( \theta = 0 \Rightarrow \cos{\theta} = 1 \), so we get \( \vec{x} \cdot \vec{y} = \vec{x} \cdot \alpha \vec{x} = \) by equations (3) and (1) above

$$ \begin{align} &\alpha {\lVert \vec{x} \rVert}^2 &&= \\ &| \alpha | \lVert \vec{x} \rVert \lVert \vec{x} \rVert &&= \\ &\lVert \vec{x} \rVert ( |a| \lVert{x} ) &&= \\ \end{align} $$

by equation (4)

$$ \begin{align} &\lVert \vec{x} \rVert \lVert \alpha \vec{x} \rVert &&= \\ &\lVert \vec{x} \rVert \lVert \vec{y} \rVert &&= \\ &\lVert \vec{x} \rVert \lVert \vec{y} \rVert \cos{\theta} \\ \end{align} $$

So that case is taken care of. Case (b) is similar, but this time \( \alpha < 0 \). The proof is nearly exactly like it was last time, except that \( \theta = \pi \) (i.e. \(180^{\circ} \) ), so \( \cos{\theta} = \cos{\pi} = -1 \) and \( \alpha = -| \alpha| \). So that case also works out.

Now we can assume that \( 0 \lneq \theta \lneq \pi \), which means that \(\vec{x} \) and \( \vec{y} \) lie in a two-dimensional plane. We’ll first consider case (c), where \( \theta = \frac{\pi}{2} \). Consider the right triangle

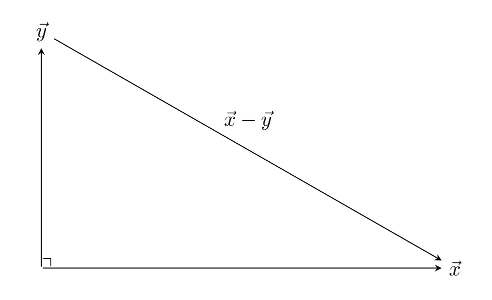
generated by \( \vec{x} \), \(\vec{y} \), and \( \vec{x} - \vec{y} \). Let’s calculate \( {\lVert \vec{x} - \vec{y} \rVert}^2 \) two different ways. The first is from equation (1) above \[ {\lVert \vec{x} - \vec{y} \rVert}^2 = (\vec{x} - \vec{y}) \cdot (\vec{x} - \vec{y}) \] by (5) and (3) (with \(\alpha = -1\)) we get

$$ \begin{align} &(\vec{x} - \vec{y}) \cdot ( \vec{x} - \vec{y} ) = \\ &\vec{x} \cdot (\vec{x} - \vec{y}) - \vec{y} \cdot (\vec{x} - \vec{y}) \\ \end{align} $$

By applying (2) and (5) both a couple of times, we get that it’s equal to

\[ \vec{x} \cdot \vec{x} - 2\vec{x} \cdot \vec{y} + \vec{y} \cdot \vec{y} \]

Now let’s calculate \( {\lVert \vec{x} - \vec{y} \rVert}^2 \) using the Pythagorean Theorem. Using that we get that it’s equal to \( { \lVert \vec{x} \rVert }^2 + { \lVert \vec{y} \rVert }^2 \), which from (1) is equal to \( \vec{x} \cdot \vec{x} + \vec{y} \cdot \vec{y} \). Setting $$ \begin{align} &\vec{x} \cdot \vec{x} - 2\vec{x} \cdot \vec{y} + \vec{y} \cdot \vec{y} &&= \\ &\vec{x} \cdot \vec{x} + \vec{y} \cdot \vec{y} \\ \end{align} $$

we get that

$$ \begin{align} &-2\vec{x} \cdot \vec{y} &&= 0 \\ &\Rightarrow \vec{x} \cdot \vec{y} &&= 0 \\ \end{align} $$

So case (c) has shown us that if \( \theta = \frac{\pi}{2} \), then \( \vec{x} \cdot \vec{y} = 0 \). In fact, because the Pythagorean Theorem works both ways (i.e. it is really an “if and only if” statement), and because the algebra works both ways, we can actually show that the dot product equals 0 if and only if the angle equals \(\frac{\pi}{2} \). Now we consider case (d), the final case.

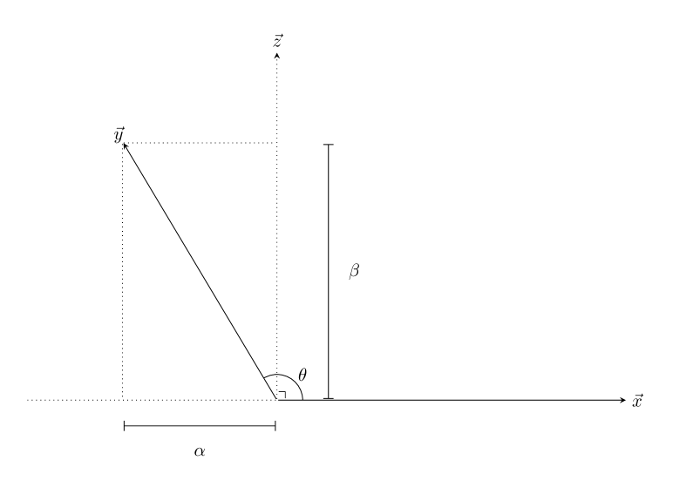
In the above image, \( \vec{z} \) is at a right angle to \( \vec{x} \), and is in the two-dimensional plane containing \( \vec{x}\) and \( \vec{y} \). We notice that we can set \[ \vec{z} := -(\frac{\vec{x} \cdot \vec{y}}{\vec{x} \cdot \vec{x}}) \vec{x} + \vec{y} \tag{6}\label{6} \] and from that we get $$ \begin{align} \vec{z} \cdot \vec{x} &= (-(\frac{\vec{x} \cdot \vec{y}}{\vec{x} \cdot \vec{x}}) \vec{x} + \vec{y}) \cdot \vec{x} \\ &= ( -\frac{ \vec{x} \cdot \vec{y} }{ \vec{x} \cdot \vec{x} } ) \vec{x} \cdot \vec{x} + \vec{x} \cdot \vec{y} \\ &= 0 \\ \end{align} $$

and \[ \vec{y} = \vec{z} + ( \frac{ \vec{x} \cdot \vec{y} }{ \vec{x} \cdot \vec{x} } ) \vec{x} \tag{7}\label{7} \] so we’ve shown that we can make this work. Now we’re going to re-write this slightly. We’re assuming that \( \vec{x} \neq \vec{0} \), but we can’t say that for sure about \( \vec{z} \), but we can still rewrite (7) as \[ \vec{y} = \frac{ \vec{x} \cdot \vec{y} }{ \vec{x} \cdot \vec{x} } \lVert \vec{x} \rVert (\frac{ \vec{x} }{ \lVert \vec{x} \rVert }) + \vec{z} \tag{8}\label{8}\] Using equation (8) with the above picture we see that \( \alpha \), the length of the component of \( \vec{y} \) in the direction of \( \vec{x} \), is equal to

\[ \frac{ \vec{x} \cdot \vec{y} }{ \vec{x} \cdot \vec{x} } \lVert \vec{x} \rVert \]

which, when combined with equation (1) from above, we see is equal to

\[ \frac{ \vec{x} \cdot \vec{y}} {\lVert \vec{x} \rVert} \]

We’re also assuming that \( \vec{y} \neq \vec{0} \), so we can write \[ \vec{y} = \lVert \vec{y} \rVert \frac{ \vec{y} }{ \lVert \vec{y} \rVert } \tag{9}\label{9} \] Using equation (9) we see that \( \alpha = \cos{ \theta } \lVert \vec{y} \rVert \). Setting both of those equations for \( \alpha \) together we get

$$ \begin{align} &\frac{ \vec{x} \cdot \vec{y}} {\lVert \vec{x} \rVert} &&= \cos{ \theta } \lVert \vec{y} \rVert \Rightarrow \\ &\vec{x} \cdot \vec{y} &&= \cos { \theta } \lVert \vec{x} \rVert \lVert \vec{y} \rVert \end{align} $$ QED

You may want to check for yourself that \( \vec{y} \neq \vec{0} \Rightarrow \lVert \vec{y} \rVert \gneq 0 \).