Even Permutations and Some Simple Non-Abelian Groups

In this entry, we’re going to prove that \(A_n\), the subgroup of all even permutations on \(n\) symbols is simple. Recall that a subgroup \(H\) of \(G\) is a normal subgroup (written \(H \trianglelefteq G\)) if and only if \( gHg^{-1} = H\), for all \(g \in G\).

We should point out a subtlety in how we’ve used this symbol. \(N \triangleleft G\) often means that \(N\) is a proper normal subgroup of \(G\) – i.e. that \(N\) is not equal to \(G\). However, we’ve been using it (in previous entries) to mean that “\(N\) is a normal subgroup of \(G\) and it might be equal to \(G\)”. We’re going to switch to using the more standard notation, and instead write \(N \trianglelefteq G\) for that, instead. Sorry for the inconvenience.

Let’s get started. We begin, as usual, with some lemmas.

Lemma 1

Proof

First, notice that for any 3-cycle \( (x, y, z) \), it’s inverse, \((x,y,z)^{-1}\) is equal to \( (x, z, y) \).

Second, notice that \(Sign( (x,y,z) ) = 1 \), so every 3-cycle (in \(S_n\)) is an even permutation, and thus belongs to \(A_n\). (proven here)

Now, since \(n \geq 5\), there are at least two symbols which do not appear in \( (a,b,c)\), let’s call them \(i\) and \(j\). Since \(H \trianglelefteq G \), we must have \[ (a, i , j)(a, b, c)(a, i, j)^{-1} \] \[ = (a,i,j)(a,b,c)(a, j, i) \] \[ = (b, c, i) \in H \tag{1}\label{1} \]

Further, notice that since \(H\) is a subgroup, that \( (a,b,c)^{-1} = \) \( (a,c,b) \in H\), so a similar calculation to what we just did above shows that \( (c,b,i) \in H \).

Similarly, using \( (b, i, j) \) and \( (c, i, j) \), we can show that \( (c, a, i) \), \( (a, c, i) \), \( (a, b, i) \) and \( (b, a, i) \) are all in \(H\).

Going even further, by starting with \( (a, j, i)\), instead, we can show all of the above 3-cycles with \(j\) instead of \(i\) are also in \(H\).

Ultimately, since \(i\) and \(j\) we arbitrarily chosen symbols not in \( (a,b,c)\), we can show that every 3-cycle with exactly two of \(a\), \(b\), or \(c\) is in \(H\).

Since every 3-cycle with exactly two of \(a\), \(b\), or \(c\) is in \(H\), we have

\[ (a, b, j)(b, a, i) = (a, i, j) \in H \tag{2}\label{2} \]

Since \(H\) is a subgroup.

Again, \(a\) can be replaced by \(b\) or \(c\) in the above equation. We can also swap the order of, \(i\) and \(j\), or replace either (or both of) them with any other symbol(s) not equal to \(a\), \(b\), or \(c\), which means we’ve now shown that \(H\) contains every 3-cycle with exactly one of \(a\), \(b\), or \(c\).

Since there are only 5 symbols, at least one of them in a 3-cycle must be \(a\), \(b\), or \(c\). Thus, when \(n = 5\), \(H\) contains every 3-cycle

Now, suppose that \(n > 5\), and let \(k\) be another symbol.

Since \(H\) contains every 3-cycle with exactly one of \(a\), \(b\), or \(c\), we have \[ (a, k, i)(a, i, j) = (i, j, k) \in H \tag{3}\label{3}\]

Since \(i\), \(j\), and \(k\) can be any symbols not equal to \(a\), \(b\), or \(c\), we have shown that \(H\) contains all of the 3-cycles with no symbols in common with \( (a,b,c)\).

Therefore, \(H\) contains every 3-cycle in \(S_n\).

QED

Lemma 2 (product of 2-cycles)

Note: this factorization is not unique, and in general these will not be disjoint 2-cycles.

Proof

We know from the Disjoint Cycles Theorem that we can break down a permutation into disjoint cycles. Generally, those cycles will not be 2-cycles. However, all we have to do is show that each k-cycle can be factored into a product of 2-cycles and we’ll have our result.

First notice that if the length of the cycle is \(1\), so that the cycle is equal to \((a)\), then since \(n \geq 2\), there is another symbol not equal to \(a\). Call it \(b\). Then, \( (a,b)(a,b) = (a)\), because they both fix everything.

Second, if the length of the cycle is \(2\), we’re okay.

Third, notice that for \(k > 2\), we have

\[ (a_1, a_2, … a_k) \] \[ = (a_k, a_{k-1})(a_k, a_{k-2}) … (a_k, a_2)(a_k, a_1) \tag{4}\label{4} \]

Remember, permutation composition, like function composition, goes from right to left. Notice that first, \(a_k\) goes to \(a_1\), which is where it should go. This means that \(a_k\) is the first element which is taken care of. Then \(a_1\) goes to \(a_k\) and then from \(a_k\) to \(a_2\) in the second product from the right. By the end, every element from \(a_1\) to \(a_{k-2}\) will go “through” \(a_k\) to get to the right element. Then, finally, on the far left, \(a_{k-1}\) goes to \(a_k\). They are then all taken care of.

This shows that each k-cycle can be broken down into a product of 2-cycles

QED

Lemma 3 (pair of 2-cycles equals product of 3-cycles)

Note: Once again, these 3-cycles will not in general be disjoint cycles.

Proof

There are three possibilities for the pair of 2-cycles

1. They share both symbols. This means that the pair is of the form \( (a,b)(a,b)\), which is the identity. Since \(n \geq 4\) there is another symbol, let’s call it \(c\), so we can replace the pair with \( (a,b,c)(a,b,c)\).
2. They share one symbol. So the pair is of the form \( (a,b)(a,c)\). This is equal to the 3-cycle \( (a,c,b) \).
3. They share no symbols. In this case they are of the form \((a,b)(c,d)\). This is also fine, as they are equivalent to \((a,d,c)(a,b,c)\).

That takes care of all of the possibilities.

QED

Lemma 4 (long cycle implies 3-cycle)

(We’ll end up using this lemma a few times in the proof of the following corollary.)

Proof

Let \(c_l\) represent the cycle of length \(l\), so that \(c_l = (a_1, a_2, … a_l) \). Then we have

\[ \rho = c_l \cdot \sigma \tag{5}\label{5} \]

where \(\sigma\) is the product of all of the other cycles of \(\rho\) not equal to \(c_l\). Since \(N \trianglelefteq A_n\), and \( (a_1, a_2, a_3)\) is an even permutation and therefore an element of \(A_n\), we can conjugate \(\rho\) by \( (a_1, a_2, a_3) \) and obtain an element of \(N\). Thus

\[ (a_1, a_2, a_3) \cdot \rho \cdot (a_1, a_3, a_2) = \pi \tag{6}\label{6} \]

is an element of \(N\). Combining equations (5) and (6) above we get

\[ \pi = (a_1, a_2, a_3) \cdot c_l \cdot \sigma \cdot (a_1, a_3, a_2) \tag{7}\label{7} \]

Since \(a_1\), \(a_2\) and \(a_3\) are all elements of cycle \(c_l\) and \(\sigma\) is the product of the other disjoint cycles of \(\rho\), \(\sigma\) fixes \(a_1\), \(a_2\) and \(a_3\). Therefore, it commutes with \( (a_1, a_3, a_2) \), \(c_l\), and \( (a_1, a_2, a_3) \), which gives us

\[ \pi = (a_1, a_2, a_3) \cdot c_l \cdot (a_1, a_3, a_2) \cdot \sigma \tag{8}\label{8} \]

Since \(N\) is a group, \( \rho \cdot \pi^{-1} \) must also be an element of \(N\). Notice that

\[ \pi^{-1} = \sigma^{-1} \cdot (a_1, a_2, a_3) \cdot c_l^{-1} \cdot (a_1, a_3, a_2) \tag{9}\label{9}\]

We can calculate \( \rho \cdot \pi^{-1}\) by using equations (5) and (9). Notice that the \(\sigma^{-1}\) in equation (9) will cancel with the \(\sigma\) in equation (5). This gives us

\[ \rho \cdot \pi^{-1} = c_l \cdot (a_1, a_2, a_3) \cdot c_l^{-1} \cdot (a_1, a_3, a_2) \tag{10}\label{10} \]

Let’s compute where \(a_1\) gets sent to together.

First it is sent to \(a_3\) (starting from the far right, since we’re composing permutations), then in \(c_l^{-1}\) it is sent to \(a_2\). Then, moving one more group to the left, it is sent to \(a_3\) again. Finally, in \(c_l\) on the far left, it is sent to \(a_4\). When you calculate out the rest, you get

\[ \rho \cdot \pi^{-1} = (a_1, a_4, a_2) \tag{11}\label{11} \]

Therefore, \(N\) has a 3-cycle.

QED

Theorem (A_n is simple when n >= 5)

Proof

Suppose that \(N \trianglelefteq A_n\). We will prove two facts:

1. Every permutation in \(A_n\) can be rewritten as the product of 3-cycles
2. \(N\) contains every 3-cycle.

Proof of 1:

By lemma 2 above, every element of \(S_n\) can be written as a product of 2-cycles. Therefore, since \(A_n \leq S_n\), every element of it can also be written as a product of 2-cycles. Recall from Theorem (sign of k-cycle), that a 2-cycle, will have \(Sign = -1\). Every element of \(A_n\) has \(Sign = 1\) (by definition), so no matter how we factor a permutation in \(A_n\) into a product of 2-cycles there must be an even number of them (this is where the term “even permutation” comes from).

By lemma 3 each pair of 2-cycles can be re-written as a product of 3-cycles. This finishes the proof of 1.

Proof of 2:

By lemma 1 all we need to do is prove \(N\) contains at least one 3-cycle. It’s not as easy as it sounds at first.

Recall that

\[ \text{fix}(\rho) := \{ x \in X | \rho(x) = x \}\]

Let \(\rho \in N\) be such that no other permutation – except for the identity – fixes more elements. Suppose \(\rho \) only has 2-cycles, except for the elements which it fixes, if there are any. First suppose there are no fixed points, so we have

\[ \rho = (a_1, a_2) \cdot (a_3, a_4) \cdot (a_5, a_6) \cdot … \]

because \(n \geq 5\), and every element belongs to a 2-cycle.

(In what we do next, we will be making an argument very similar to what we did in the proof of lemma 4, just above. Because this argument is so similar, we will not be as thorough.)

Then, since \(N \trianglelefteq A_n\), we can conjugate \(\rho\) by the 3-cycle \( (a_1, a_3, a_5) \) to obtain

\[ (a_1, a_3, a_5) \cdot (a_1, a_2) \cdot (a_3, a_4) \cdot (a_5, a_6) \cdot (a_1, a_5, a_3) \cdot … \]

which must be an element of \(N\).

That is equal to

\[ \pi = (a_1, a_6) \cdot (a_2, a_3) \cdot (a_4, a_5) \cdot … \]

(In the proof of lemma 4, we calculated \( \rho \cdot \pi^{-1} \), however here, since every cycle is a 2-cycle, \(\pi = \pi^{-1}\), so we’ll omit the inverse)

This gives us

\[ \rho \cdot \pi = (a_1, a_5, a_3)(a_2, a_4, a_6) \tag{12}\label{12} \]

is an element of \(N\). This is impossible, however, because we assumed that no other permutation fixed more elements than \(\rho\). \(\rho \cdot \pi\), however, fixes \(a_7\) and \(a_8\), which \(\rho\) cannot, since it is composed of an even number of 2-cycles and therefore contains at least four 2-cycles.

Therefore, if \(\rho\) consists entirely of 2-cycles, it must have exactly two 2-cycles.

Now, suppose \(\rho = (a_1, a_2) \cdot (a_3, a_4) \).

As we did before, \( (a_1, a_3, a_5) \in A_n\), and \(N\) is a normal subgroup, so \[ \pi = (a_1, a_3, a_5) \cdot (a_1, a_2) \cdot (a_3, a_4) \cdot (a_1, a_5, a_3) \] which is equal to \[ (a_2, a_3) \cdot (a_4, a_5) \] Then, taking the composition, \( \rho \cdot \pi \) gives us \[ (a_1, a_2, a_4, a_5, a_3) \] Which, by lemma 4, above, implies that \(N\) has a 3-cycle.

So far we’ve shown that if \(N\) contains a permutation which is only the product of 2-cycles, then it also must contain a 3-cycle.

Lemma 4 shows us that if \(N\) contains a permutation with a cycles longer than \(4\), it must also contain a 3-cycle, so now suppose that it contains a permutation with more than one 3-cycle.

Then

\[ \rho = (a_1, a_2, a_3) \cdot (a_4, a_5, a_6) \cdot … \]

Once again, we have \( (a_1, a_4, a_5) \in A_n\), so the product

\[ \pi = (a_1, a_4, a_5) \cdot (a_1, a_2, a_3) \cdot (a_4, a_5, a_6) \cdot (a_1, a_5, a_4) \cdot … \]

is also in \(N\).

Computing \( \rho \cdot \pi^{-1}\) gives us

\[ (a_1, a_4, a_2, a_6, a_5) \]

which must be a permutation in \(N\). By lemma 4 above, this implies that \(N\) contains a 3-cycle.

The only other case to consider is when \(N\) contains a 3-cycle. In that case, we are done.

QED

The best-known corollary of this theorem comes from Galois Theory (Wikipedia), which we’ll get to later. That’s the theorem that shows that it’s impossible to solve the general quintic equation with radicals. However, since we’ve proven the Jordan-Holder Theorem, we’re able to prove another result about the impossibility of finding a different type of equation.

Before we do that, though, we’ll have to briefly introduce roots of unity.

Definition (n_th roots of unity)

For example, \(1\) is a 1^st root of unity (not very interesting, though), \( \{1, -1 \} \) is the set of 2^nd roots of unity. The 3^rd roots of unity look like this

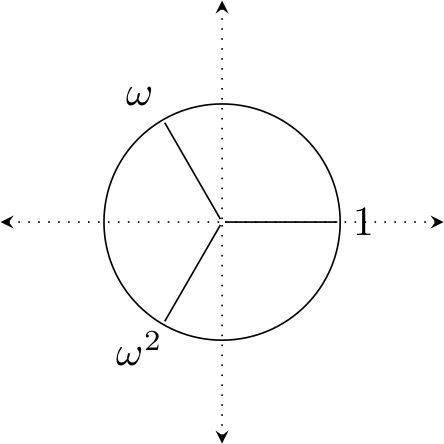
We’ve drawn the unit circle as well. Every n^th root of unity for every n will lie on that circle (it is afterall, called the unit circle). The horizontal dotted line represents the real number line, while the vertical dotted line represents the imaginary number line.

This means that two of the three 3^rd roots of unity don’t lie on the real number line. The set of 3^rd roots of unity is \( \{ 1, \omega, \omega^2 \} \), where \(\omega = -\frac{1}{2} + \frac{\sqrt{3}}{2}i\), and \(\omega^{2} = -\frac{1}{2} - \frac{\sqrt{3}}{2}i\).

The n^th roots of unity form a group under multiplication, with identity element equal to 1. The group is cyclic. We’ll prove this in a later entry.

This is enough of an intro to roots of unity for the result we’re going to prove.

Recall the definition of \(Sign(\sigma)\), where \(\sigma \in S_n\) (defined here).

Notice that \(Sign\) is a family of homomorphisms from \(S_m\) into the set \(\{1, -1\} \). We just saw that that set is equal to the group of the 2^nd roots of unity. It’s natural to wonder whether it’s possible to find other families of homomorphisms \( \phi_{m,n} : S_m \rightarrow \mathcal{R}_n\), where \(\mathcal{R}_n\) is the set of n^th roots of unity, and \(m \geq n\). It turns out that this is impossible when \(n > 2\).

Corollary (no analogous complex Sign)

Proof

Suppose there were such a \(\phi_{m,n} : S_m \rightarrow \mathcal{R}n\), then by this theorem the kernel of \(\phi{m,n}\) would be a normal subgroup of \(S_m\). It would have index \(n\).

This means that \(S_m\) would have a chain of subnormal subgroups like \[ S_m \triangleright \ker(\phi_{m,n}) \triangleright … \triangleright \{e\} \tag{13}\label{13}\]

However, when we proved that \(A_m\) is a simple group (because \(m \geq 5\)) we showed that \(S_m\) has a chain of subnormal subgroups that is exactly equal to

\[S_m \triangleright A_m \triangleright \{e\} \tag{14}\label{14}\]

which cannot possibly be made any longer.

By the Jordan-Holder Theorem those two chains will produce sets of factor groups which are equal up to isomorphisms and reordering, but this is impossible to do with (13) and (14) because the chain in (14) produces a set of exactly two factor groups, namely

\[ \{ \mathbb{Z}_2, A_m\} \tag{15}\label{15}\]

where \( \mathbb{Z}_2 = S_m / A_m \) and \( A_m = A_m / \{e\}\).

However, the chain from (13) above will generate a set of factor groups containing \( \mathbb{Z}_n = S_{m} / {\ker(\phi_{m,n})}\). Therefore, the two sets can’t be equal, and we have achieved a contradiction, so there cannot be such a family of homomorphisms.

QED

That’s it for this entry. Bye!