Fibonacci Numbers, and some more of the Euclidean Algorithm and RSA.

The last couple entries have featured the Euclidean Algorithm. We proved that it returns the/a greatest common divisor of two ring elements. Here we’re going to start out by analyzing the number of steps it takes to finish. We’re going to restrict our focus to the ring of integers, \( \mathbb{Z} \).

In order to get an upper bound on the number of steps the Euclidean Algorithm takes to finish, we want to consider pairs of integers which take the most steps for their size. That is, we want to find pairs, \( a, b \in \mathbb{Z} \), such that for any other pair of integers, \( x, y \in \mathbb{Z}\), where \( x, y \leq \max(a,b) \), \( T(x,y) \leq T(a,b) \), where \( T(n,m) \) is the number of divisions the Euclidean Algorithm will require to find \( \gcd(n,m) \). We can do this by running the Euclidean Algorithm backwards.

We can run it backwards by working the matrix equation

$$ \begin{bmatrix} &x_{i+1} \\ &x_{i+2} \\ \end{bmatrix}:= \begin{bmatrix} &0 & 1 \\ &1 & -f_i \\ \end{bmatrix} \begin{bmatrix} &x_{i} \\ &x_{i+1} \\ \end{bmatrix} $$

backwards.

Recall from the Euclidean Algorithm that we defined

$$ M_i := \begin{bmatrix} &0 & 1 \\ &1 & -f_i \\ \end{bmatrix} $$

where \(\displaystyle f_i := \left \lfloor \frac{x_i}{x_{i+1}} \right \rfloor \). We can invert \( M_i \), and when we do we obtain

$$ M_i^{-1} = \begin{bmatrix} &f_i & 1 \\ &1 & 0 \\ \end{bmatrix} $$

and that gives us

$$ \begin{bmatrix} &x_{i} \\ &x_{i+1} \\ \end{bmatrix}= \begin{bmatrix} &f_i & 1 \\ &1 & 0 \\ \end{bmatrix} \begin{bmatrix} &x_{i+1} \\ &x_{i+2} \\ \end{bmatrix} $$

Now, we’re guaranteed that \( x_i \gneq x_{i+1} \), so \( f_i \geq 1 \). Therefore, the backward sequence \( x_n \), \( x_{n-1} \), … \( x_1 \), \( x_0 \) will grow the slowest when \( f_i = 1 \) for all \( i \). Let’s see what happens when \( x_n = 0 \), \( n_{n-1} = 1 \) and \( f_i = 1 \).

We end up with

$$ \begin{bmatrix} &x_{n - (k+1)} \\ &x_{n - k} \\ \end{bmatrix}= \begin{bmatrix} &1 & 1 \\ &1 & 0 \\ \end{bmatrix}^k \begin{bmatrix} &1 \\ &0 \\ \end{bmatrix} $$

Notice that this gives us a backward sequence where \( x_n = 0 \), \( n_{n-1} = 1 \), and \( x_{n-2} = x_{n-1} + x_n \). This is none other than the Fibonacci Sequence in reverse!

Definition: Fibonacci Sequence

Thus we see that we have the result

Corollary: Fibonacci Numbers are Euclidean Algorithm’s worst case input

Proof

Given in the discussion above.

QED

Now we’ll find a bound for the growth of the Fibonacci Sequence. In fact, we’ll do even better; we’ll find a formula for it. Essentially what we’re going to do is find a formula for \( \displaystyle \begin{bmatrix} 1 &1 \\ 1 &0 \end{bmatrix}^k \).

Suppose we could find matrices, \( P \) and \( D \), such that

$$ D = \begin{bmatrix} \alpha &0 \\ 0 &\beta \\ \end{bmatrix} $$

and

$$ \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix} = P \cdot D \cdot P^{-1} $$

then, since

$$ \begin{align} \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix}^2 &= (P \cdot D \cdot P^{-1})(P \cdot D \cdot P^{-1}) \\ &= P \cdot D^2 \cdot P^{-1} \\ \end{align} $$

and, by induction,

$$ \begin{align} \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix}^k &= P \cdot D^k \cdot P^{-1} \\ &= P \cdot \begin{bmatrix} \alpha^k &0 \\ 0 &\beta^k \end{bmatrix} \cdot P^{-1} \\ \end{align} $$

Now we’re going to find \( \alpha \), \( \beta \) and \( P \). Before we do that, though, we’re going to need a lemma.

Lemma: Inverse of 2x2 matrix

We’re pretty sure you’ve heard of the determinant of a matrix before. Recall that \( ad - bc \) is the determinant of \( P \). We will discuss them in more detail in a later entry.

Proof

We’re only allowed to divide by a unit of a ring.

Notice that \( P \cdot P^{-1} = I \), the identity matrix.

QED

Now we’ll return to our discussion of the Fibonacci Sequence. Let \( P = \begin{bmatrix} a &b \\ c &d \end{bmatrix} \), so that

$$ \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix} = P \cdot D \cdot P^{-1} $$

implies

$$ \begin{bmatrix} a &b \\ c &d \\ \end{bmatrix} \cdot \begin{bmatrix} \alpha &0 \\ 0 &\beta \\ \end{bmatrix} = \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix} \cdot \begin{bmatrix} a &b \\ c &d \\ \end{bmatrix} $$

which, when we multiply the matrices, gives us

$$ \begin{bmatrix} a \alpha &b \beta \\ c \alpha &d \beta \\ \end{bmatrix} = \begin{bmatrix} a + c &b + d \\ a & b \\ \end{bmatrix} $$

Thus we have (assuming \( \alpha, \beta \neq 0 \))

$$ \begin{align} c &= \frac{a}{\alpha} \\ d &= \frac{b}{\beta} \\ a\alpha &= a + c \\ b\beta &= b + d \\ \end{align} $$

which gives us

$$ \begin{align} a\alpha &= a + \frac{a}{\alpha} \\ b\beta &= b + \frac{b}{\beta} \\ \end{align} $$

multiplying the top equation by \( \alpha \) and the bottom equation by \( \beta \) gives us

$$ \begin{align} a\alpha^2 &= a\alpha + a \\ b\beta^2 &= b\beta + b \\ &\implies \\ a(\alpha^2 - \alpha - 1) &= 0 \\ b(\beta^2 - \beta - 1) &= 0 \\ \end{align} $$

Notice that if either \( a \) or \( b = 0 \), then \( ad - bc = 0 \), since \( c = \frac{a}{\alpha} \) and \( d = \frac{b}{\beta} \). Therefore, both \( \alpha \) and \( \beta \) are roots of the quadratic polynomial

$$ x^2 - x - 1 $$

which means, by using the quadratic formula, that

$$ \alpha, \beta = \frac{1 \pm \sqrt{5}}{2} $$

Now, computing the determinant of both sides of (equation-1), we see that

$$ \alpha \beta = b(a + c) - d(b + d) $$

and since \( a \alpha = a + c \) and \( b \beta = b + d \), we get

$$ \alpha \beta = ab( \alpha - \beta ) $$

We’ve already noted that

$$ \begin{align} \alpha &\neq 0 \\ \beta &\neq 0 \\ a &\neq 0 \\ b &\neq 0 \\ \end{align} $$

so we now know that \( \alpha \neq \beta \). Therefore, we will try setting

$$ \begin{align} \alpha &= \frac{1 + \sqrt{5}}{2} \\ \beta &= \frac{1 - \sqrt{5}}{2} \\ \end{align} $$

Finally, let’s try to figure out what \( a \), \( b \), \( c \), and \( d \) are. Notice that \( a \) determines \( c \) and \( b \) determines \( d \), but \( a \) and \( d \) don’t seem to affect each other. Let’s just try setting \( a = \alpha \) and \( b = \beta \). When we do that, we get \( c = 1\) and \( d = 1 \). It turns out that this works. It’s not the only way we could have solved it, but as long as it works, let’s use it.

Then,

$$ \begin{align} \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix}^k &= P \cdot D^k \cdot P^{-1} \\ &= P \cdot \begin{bmatrix} \alpha^k &0 \\ 0 &\beta^k \end{bmatrix} \cdot P^{-1} \\ \end{align} $$

becomes

$$ \begin{bmatrix} \alpha &\beta \\ 1 &1 \\ \end{bmatrix} \begin{bmatrix} \alpha^k &0 \\ 0 &\beta^k \\ \end{bmatrix} \begin{bmatrix} 1 &-\beta \\ -1 &\alpha \\ \end{bmatrix} \frac{1}{\alpha - \beta} = \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix}^k $$

Since \( \alpha - \beta = \sqrt{5} \), and

$$ \begin{bmatrix} y_{l+1} \\ y_{l} \\ \end{bmatrix}= \begin{bmatrix} 1 &1 \\ 1 &0 \\ \end{bmatrix}^l \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} $$

we get

$$ y_l = [ \alpha^l - \beta^l ] \frac{\sqrt{5}}{5} $$

Now, since \( |\alpha| > |\beta| \), we have \( y_l \geq \alpha^l \cdot \frac{1}{10} \). This implies that if \( n = y_l \), then \( \ln(n) = \ln(y_l) \), and

\[ \ln(y_l) \geq l\ln(\alpha) - \ln(10) \]

and since the right-hand side of that inequality represents the maximum number of divisions involved in computing the Euclidean Algorithm on an input whose maximum is \( y_l \), we see that

\[ T(m,n) \in O(\ln(\max(m,n))) \]

So, we’ve proven two nice results

Corollary: Formula for Fibonacci Sequence

Proof

In the above discussion.

QED

Corollary: The Euclidean Algorithm requires O(ln(n)) divisions

Proof

In the above discussion.

QED

---

Repeated Squaring Technique

Now we turn our focus to something we mentioned at the end of our discussion of the RSA Encryption Algorithm (You’ll see it if you scroll down to near the end of that entry). We called it “Repeated Squaring”. It probably has other names as well. It’s an extremely old technique. In fact, it’s very similar to “Duplation and Mediation”¹, a technique used by the ancient Egyptians to perform multiplication. We will show how to use it to calculate

\[ x^t \mod N \]

where \( t \) could be a large positive integer. We’ll give an example with

$$ \begin{align} N &= 1009 \cdot 1013 \\ &= 1022117 \\ x &= 1000000 \\ t &= 697 \\ \end{align} $$

We use these values to generate the table below as follows. We repeatedly divide \( s \) by \(2\) and note the remainder mod \(2\). Next, we take \(x\) and square it mod \(N\). We should also note that the algorithm doesn’t actually require us to save the entire table. All we have to do is work with it one row at a time.

We can get away with only remembering one row by also keeping an output variable. We’ll call it “\(z\)”. At the beginning of the algorithm, \( z \) will be set to \(1 \mod N\). At each row, if \( s \mod 2 \equiv 1 \), we multiply \(z\) by the value of \( x \) in the third column (what is actually \( \displaystyle x^{2^k}\), for some \(k\))

\(s\)	mod \(2\)	\(x\)
\(697\)	\(1\)	\(x^1 \equiv 1000000 \)
\(348\)	\(0\)	\(x^2 \equiv 589763\)
\(174\)	\(0\)	\( x^4 \equiv 113771\)
\(87\)	\(1\)	\(x^8 \equiv 772870\)
\(43\)	\(1\)	\(x^{16} \equiv 817866\)
\(21\)	\(1\)	\(x^{32} \equiv 765646\)
\(10\)	\(0\)	\(x^{64} \equiv 56423\)
\(5\)	\(1\)	\(x^{128} \equiv 682591 \)
\(2\)	\(0\)	\(x^{256} \equiv 483065 \)
\(1\)	\(1\)	\(x^{512} \equiv 438891\)

So, our \( z \) variable would have the following values

\(z\)
\(1\)
\(1000000\)
\(1000000\)
\(1000000\)
\( 318918 \)
\( 195992 \)
\( 427711 \)
\( 427711 \)
\( 312023 \)
\( 312023 \)
\( 850833 \)

so our algorithm will return the value \( 850833 \). Notice that none of the numbers get larger than \( N \), and it takes about \( \left \lceil \log_2 (t) \right \rceil \) steps.

It works because \( t = 1010111001_2 \). That is, \( t \) is equal to \( 1010111001 \) in base 2 (or binary). So

$$ x^{697} = x^1 x^8 x^{16} x^{32} x^{128} x^{512} $$

That’s it!

---

A few more thoughts on RSA

What this shows, is that the RSA Algorithm is fast for Alice and Bob. Each of them has to perform \( \approx \ln(N) \) divisions and multiplications. This site, for example, has an \(N\) which is about \( 2048 \) bits. The public exponent, \( e \) is only \( 24 \) bits, but it’s inverse, \( t \) is probably much much larger (probably \( \approx 2048 \) bits).

Note that if you can factor \( N = pq \), then you can find \( t \) for yourself (using the Euclidean Algorithm, which is exactly how Alice found \(t\) for the \( e \) she picked), and you could “break the encryption”. Also notice that if you can find \( t \), then you can multiply \( e \) and \( t \) to get

\[ e \cdot t = s \cdot (p-1)(q-1) + 1 \]

for some \( s \). Since

\[ c \cdot t \equiv 1 \mod (p-1)(q-1) \]

Recall that \( N = pq \) is public (so you would know it as well). You could then calculate

$$ \frac{e \cdot t - 1}{N} = s(1 - \frac{1}{q} - \frac{1}{p} + \frac{1}{pq}) $$

if \( p \) and \( q \) are extremely large, then \( s \) is the nearest integer to \( \displaystyle \frac{e \cdot t - 1}{N} \). Once you know \( s \), you can calculate

$$ \frac{e \cdot t - 1}{s} = (p-1)(q-1) $$

and once you know that, you can calculate

$$ p + q = N - (p-1)(q-1) + 1 $$

Then, you can solve the quadratic polynomial (with indeterminate, \( X \))

$$ X^2 - (p+q)X + N $$

and recover \(p\) and \(q\).

The point of all of this is that calculating \( t \) is essentially as difficult as factoring \( N \) into \(p\) and \(q\). I.e. “breaking RSA” is roughly equivalent to factoring \(N\).

I’m not going to write anything more on factoring for this entry. We’ll get to it in a later entry.

We’d also like to mention that the RSA algorithm isn’t used for bulk communication. It is only used to exchange keys for a much faster symmetric key encryption algorithm.

For a much (much!) more in-depth explanation of what actually happens when you connect to a secure website, see tlseminar.github.io/first-few-milliseconds/ which is based on this older article www.moserware.com/2009/06/first-few-milliseconds-of-https.html.

---

The Golden Mean

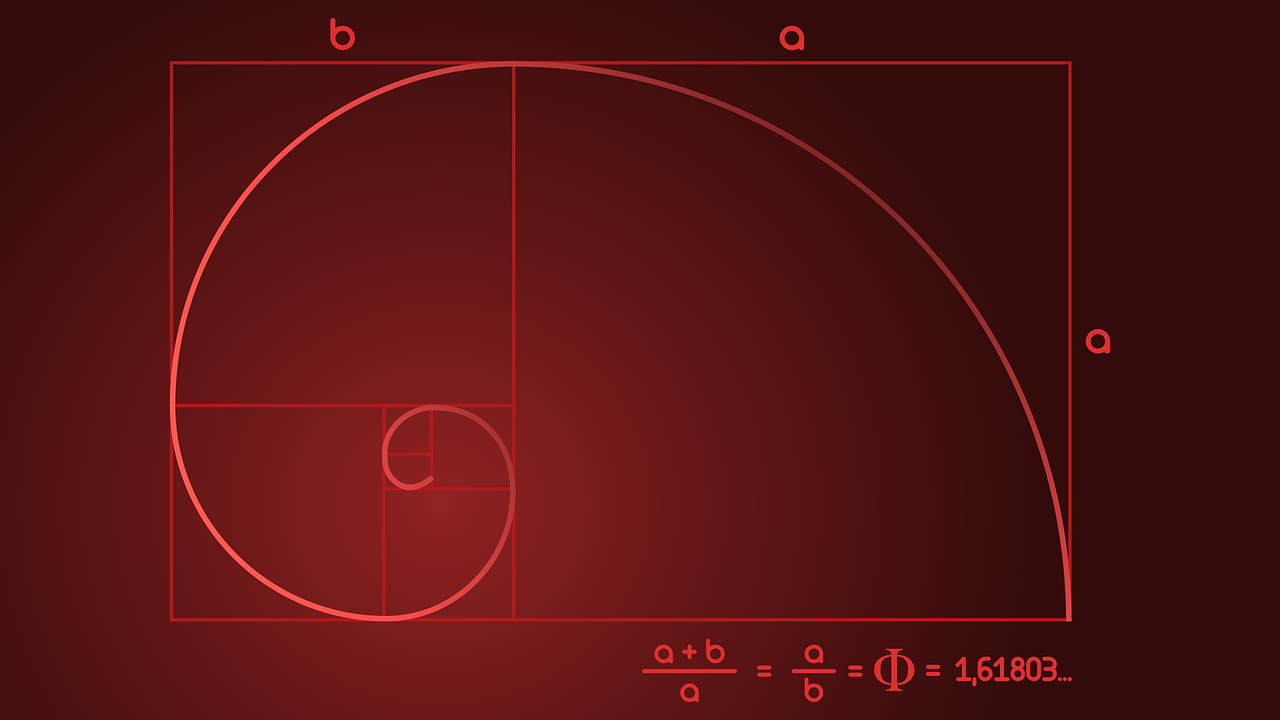
The last thing we’ll discuss in this entry is the so-called “Golden Mean”. Notice the equation in the image above (which, like most of the other images on this site, was downloaded from pixabay.com).

\[ \frac{a + b}{a} = \frac{a}{b} \]

Multiplying though by the denominators, we get

\[ a^2 = ab + b^2 \]

Let’s treat this like a polynomial with \( a \) as the indeterminate. Then we have

\[ a^2 - ba + b^2 \]

When we solve it, using the quadratic equation we get

\[ a = \frac{b}{2}(1 \pm \sqrt{5}) \]

This should look familiar from earlier Formula for the Fibonacci Sequence. It’s \( b \cdot \alpha \). Therefore, there are two possible values for \( a \): \( \alpha \cdot b \) or \( \beta \cdot b \). However, since \( a \) and \( b \) represent lengths, they have to be non-negative, so we can eliminate \( \beta \cdot b \) as a possibility. Thus,

\[ a = \alpha \cdot b \]

so what we’ve called “\(\alpha\)” is equal to the “Golden Mean”. When referring to “The Golden Mean”, “\( \Phi \)” is often used to represent it.

Finally, we’re going to show that \( \alpha \) (a.k.a “\(\Phi\)”) is equal to

\[ \lim\limits_{k \rightarrow \infty} \frac{y_{k+1}}{y_k} \]

where \( y_k \) is the \( k^{th} \) entry in the Fibonacci Sequence.

For now, let’s call the limit, “\(L\)”. That is,

\[ L := \lim\limits_{k \rightarrow \infty} \frac{y_{k+1}}{y_k} \]

Recall (from the definition of the Fibonacci Sequence) that

\[ y_{k+1} = y_k + y_{k-1} \]

which means that

$$ \begin{align} \frac{y_{k+1}}{y_k} &= \frac{y_k + y_{k-1}}{y_k} \\ &= 1 + \frac{y_{k-1}}{y_k} \\ \end{align} $$

Now, we haven’t discussed limits much on this site, and we certainly haven’t developed any theorems about them yet, but we will end up having to use one here:

\[ \lim\limits_{k \rightarrow \infty} \frac{1}{ w_k } = \frac{1}{\lim\limits_{k \rightarrow \infty} y_k } \]

when the limit exists and is finite and not zero (limits do not always exist). Thus, if the limit exists, we have

\[ L = 1 + \frac{1}{L} \]

which gives us

\[ L^2 - L - 1 = 0 \]

which means that \( L = \alpha \) or \( L = \beta \). Since \( \{ y_k \}_{k = 0}^{\infty} \) is an increasing sequence, \( L \neq \beta \). Thus, \( L = \alpha \), if it exists.

Proving the limit exists will have to wait for another entry, as will proving the result about the limit of inverses being equal to the inverse of the limit.

That’s all for now. Thanks for reading!!