Modules, Vector Spaces, and More!

We’ve already used vectors and matrices without defining them. It’s about time we treated them with a bit more rigor.
Feel free to skip over whatever you’re already familiar with.
Definition: R-Module
Let \(R\) be a ring and let \(\mathcal{M}\) be a set with the following properties.
- For any \( r \in R\), and \( m_1, m_2 \in \mathcal{M}\) we have $$ \begin{align} &1 &&r(m_1 + m_2) = rm_1 + rm_2 \in \mathcal{M} \\ &2 &&(m_1 + m_2)r = m_1r + m_2r \in \mathcal{M} \\ &3 &&m_1 + m_2 \in \mathcal{M} \\ \end{align} $$
- For any \( r_1, r_2 \in R\) and \(m \in \mathcal{M}\), we have $$ \begin{align} &1 &&(r_1 + r_2)m = r_1m + r_2m \in \mathcal{M} \\ &2 &&m(r_1 + r_2) = mr_1 + mr_2 \in \mathcal{M} \\ \end{align} $$ \(\mathcal{M}\) is said to be a module over \(R\).
If only 1.1 and 2.1 hold, then \(\mathcal{M}\) is said to be a right module over \(R\). Similarly, if only 1.2 and 2.2 hold, then \(\mathcal{M}\) is said to be a left module over \(R\).
Definition: F-Vector Space
A module over a field is called a vector space.
Definition: R-Algebra
Let \(\mathcal{A}\) be a Vector Space over a ring with unity \(R\). If \(\mathcal{A}\) is also a ring with unity, such that for all \(r \in R\) and \(a_1, a_2 \in \mathcal{A}\) we have
\( (ra_1)a_2 = r(a_1a_2) = a_1(ra_2) \), then \(\mathcal{A}\) is said to be an algebra over \(R\), or an \(R\)-algebra.
Notice that a ring is a trivial module over itself. Similarly a field is a trivial vector space and algebra over itself.
Definition: Matrix
Let \(R\) be a ring. A Matrix, \(M\) is a 2-dimensional array of elements of \(m_{i,j}\) of \(R\), where for each \(i\), the 1-dimensional array \(m_{i,j}\) where \(j = 1, 2, …\) has the same length. The length is not necessarily finite. Likewise, for each \(j\), the one dimensional array \(m_{i,j}\), where \(i = 1, 2, …\) has the same length.
It is common to write the \(i^{th}\) row of \(M\) as \((m_{i })\), and the \(j^{th}\) column of \(M\) as \((m_{ j})\).
They are usually written so that the \(i\)’s index rows and the \(j\)’s index columns. For example
$$ M = \begin{pmatrix} m_{1,1} & m_{1,2} & … & \\ m_{2,1} & m_{2,2} & … & \\ \vdots & \vdots & \ddots & \\ \end{pmatrix} $$
We might also write
\[ M = (m_{i,j}) \]
If the length of both the rows and columns are finite, then \(M\) is a finite-dimensional matrix.
If the length of each column of \(M\) is \(s\) (so there are \(s\) rows) and the length of each row of \(M\) is \(t\) (so there are \( t \) columns), then \(M\) is said to be an \(s \times t\) (read “\(s\) by \(t\)”) matrix. This is often written
\[ M_{s,t} \]
The set of all \(s \times t\) matrices with entries in ring \(R\) is an \(R\)-module. It is often written \( R^{s \times t} \). The rule for adding two matrices is
$$ \begin{align} &\begin{pmatrix} a_{1,1} & a_{1,2} & … & a_{1, t} \\ a_{2,1} & a_{2,2} & … & a_{2, t} \\ \vdots & \vdots & \ddots & \vdots \\ a_{s,1} & a_{s, 2} & … & a_{s, t} \\ \end{pmatrix} + \begin{pmatrix} b_{1,1} & b_{1,2} & … & b_{1, t} \\ b_{2,1} & b_{2,2} & … & b_{2, t} \\ \vdots & \vdots & \ddots & \vdots \\ b_{s,1} & b_{s, 2} & … & b_{s, t} \\ \end{pmatrix} \\ \\ &= \begin{pmatrix} a_{1,1} + b_{1,1} & a_{1,2} + b_{1,2} & … & a_{1,m} + b_{1,t} \\ a_{2,1} + b_{2,1} & a_{2,2} + b_{2,2} & … & a_{2,m} + b_{2,t} \\ \vdots & \vdots & \ddots & \vdots \tag{1}\label{1} \\ a_{s, 1} + b_{s, 1} & a_{s,2} + b_{s,2} & … & a_{s,t} + b_{s, t} \\ \end{pmatrix} \end{align} $$
This can be written more succinctly as
\[ (a_{i,j}) + (b_{i,j}) = (a_{i,j} + b_{i,j}) \tag{2}\label{2} \]
The rule for multiplying by an element of \(R\) is
\[ r(a_{i,j}) = (ra_{i,j}) \tag{3}\label{3} \]
What’s much more interesting is that if \(s = t\) and \(R\) is a ring with unity, then \(R^{s \times s}\) is an \(R\)-algebra. In fact, even if \(R\) isn’t a ring with unity we can still define multiplication between two elements of \(R^{s \times s}\). This is the usual matrix multiplication it is defined so that
\[ (a_{i,j}) \cdot (b_{i,j}) = \left ( \sum\limits_{k=1}^{s}{ a_{i,k}b_{k,j} } \right ) \tag{4}\label{4} \]
However, just because we’ve said that this is how it should work doesn’t mean that it will all work out. We have to prove that this gives \(R^{s \times s}\) a ring structure. In order to do that, we have to verify that all of the ring axioms hold.
It’s easy to see that all of the ones involving \(+\) hold, since \(+\) works component-wise. For example, \(+\) in \(R^{s \times s}\) is associative because \( ((a_{i,j}) + (b_{i,j})) + (c_{i,j}) \) is equal to \( (a_{i,j}) + ((b_{i,j}) + (c_{i,j})) \).
Matrix “multiplication” (the \( \cdot \) operator for \(R^{s \times s}\)) isn’t obviously associative, and it’s also not obvious that it distributes with matrix \(+\). We’ll prove both of those next.
Lemma: Matrix multiplication is associative
Let \( (a_{i,j}) \), \((b_{i,j})\), and \( (c_{i,j}) \) be elements of \(R^{s \times s}\), where \(R\) is a ring. Then
$$ \begin{align} &((a_{i,j}) \cdot (b_{i,j})) \cdot (c_{i,j}) \\ = &(a_{i,j}) \cdot ((b_{i,j}) \cdot (c_{i,j})) \tag{5}\label{5} \end{align} $$
Proof
By definition, the left-hand side of the equation is equal to
\[ \left ( \sum\limits_{k=1}^{s} {a_{i,k}b_{k,j}} \right) \cdot (c_{i,j}) \tag{6}\label{6} \]
which is equal to
\[ \left ( { \sum\limits_{l=1}^{s} \left \{ \sum\limits_{k=1}^{s} { a_{i,k}b_{k,l} } \right \} c_{l, j} } \right ) \tag{7}\label{7} \]
and that is equal to
\[ \left ( { \sum\limits_{k, l = 1 }^{s} a_{i,k}b_{k,l}c_{l,j} } \right ) \tag{8}\label{8} \]
On the other hand, the right-hand side of equation (5) is equal to
\[ (a_{i,j}) \cdot \left ( { \sum\limits_{l=1}^{s} { b_{i,l}c_{l,j} } } \right ) \tag{9}\label{9}\]
where we’ve kept the bound variable \( l \) for the sum between \( (b_{i,j})\) and \( (c_{i,j}) \), which is perfectly fine, since it’s the variable we’re summing over.
equation (9) is equal to
\[ \left ( \sum\limits_{k=1}^{s} a_{i,k} \left \{ \sum\limits_{l=1}^{s} { b_{k,l}c_{l,j} } \right \} \right ) \tag{10}\label{10} \]
Now, when we evaluate equation (10), we once again end up with equation (8). Therefore, the two sides of equation (5) are equal.
QED
Now let’s verify that the distributive laws hold
Lemma: Matrix multiplication distributes
Let \( A \), \(B\), and \(C\) be elements of \(R^{s \times s}\), then
- \(A (B + C) = AB + AC \)
- \( (B + C)A = BA + CA \)
Proof
The proofs are nothing more than applying definitions and pushing symbols. We’ll provide the proof for case 1. The other case is nearly identical.
$$ \begin{align} A(B + C) &= (a_{i,j}) \left ( (b_{i,j}) + (c_{i,j}) \right ) \tag{11}\label{11} \\ &= (a_{i,j})( b_{i,j} + c_{i,j} ) \tag{12}\label{12} \\ \end{align} $$
by the definition of addition in \(R^{s \times s}\). Applying the definition of multiplication to (11), we obtain
\[ \left ( \sum\limits_{k=1}^{s} a_{i,k}(b_{k,j} + c_{k,j}) \right ) \tag{13}\label{13} \]
which is equal to
\[ \left ( \sum\limits_{k=1}^s a_{i,k}b_{k,j} + \sum\limits_{k=1}^s a_{i,k}c_{k,j} \right ) \tag{14}\label{14} \]
which can be separated as
$$ \begin{align} & \left ( \sum\limits_{k=1}^s a_{i,k}b_{k,j} \right ) + \\ & \left ( \sum\limits_{k=1}^s a_{i,k}c_{k,j} \right )\tag{15}\label{15} \end{align} $$
by the definition of addition in \(R^{s \times x}\) in the opposite direction as we applied it in (12). Then, applying the definition of multiplication in the opposite direction to what we did to go from (12) to (13), we get
\[ (a_{i,j})(b_{i,j}) + (a_{i,j})(c_{i,j}) \tag{16}\label{16} \]
which is just different notation for
\[ AB + AC \]
QED
This finishes the proof that \(R^{s \times s}\) is a ring. If \(1 \in R\) (where \(1\) is the unique element such that \(1 \cdot x = x \cdot 1 = x\), for all \(x \in R \)), then \( I = (\delta_{i,j}) \) is the identity element of \(R^{s \times s}\), where $$\delta_{i,j} = \begin{cases} 1, i = j \\ 0, i \neq j \end{cases} $$
This will be familiar to anyone who has encountered Matrices before. Now we’ll prove that it is actually the identity.
Mini-lemma: the identity matrix
Let \(R\) be a ring with identity, then \(I = \delta_{i,j}\) is the identity element of \(R^{s \times s}\).
Proof
We’ll prove \(IM = M\), the other way is nearly the same.
$$ \begin{align} & (\delta_{i,j})(m_{i,j}) \\ &= \left ( \sum\limits_{k = 1}^{s} { \delta_{i,k}m_{k,j} } \right ) \\ &= (m_{i,j}) \end{align} $$
QED
Now we’re going to switch focus slightly and prove a result about the structure of the lattice of a module and its submodules.
In an earlier entry, we gave the definition of a modular lattice, and then we proved some theorems about how well-behaved they are. Here we’re going to prove that the lattice of submodules of a given module is modular (we think this is where the name comes from).
Theorem: Lattice of submodules is modular
Let \(\mathcal{L}_{\mathcal{V}}\) be the lattice of submodules of a module, \(\mathcal{V}\). Then \(\mathcal{L}_{\mathcal{V}}\) is modular. That is, there is no sub-lattice like this
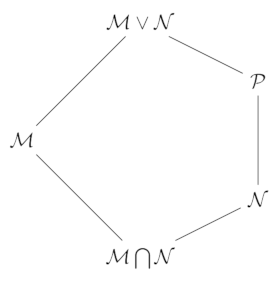
Where
$$ \begin{align} \mathcal{M} \vee \mathcal{N} &= \mathcal{M} \vee \mathcal{P} \\ \mathcal{M} \wedge \mathcal{N} &= \mathcal{M} \wedge \mathcal{P} \tag{17}\label{17} \\ \mathcal{N} \subsetneq \mathcal{P} & \end{align} $$
Proof
The proof is fairly easy. It relies mostly on proving the following claim. Let \( \mathcal{M} \) and \( \mathcal{N} \) be modules over a ring, \(R\). Then
$$ \mathcal{M} \vee \mathcal{N} = \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} \tag{18}\label{18} $$
To see why (18) holds, notice first, that
$$ \mathcal{M} \vee \mathcal{N} \supseteq \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} $$
because \( \mathcal{M} \vee \mathcal{N} \) is an Abelian group under the addition operator (\( + \)), and since both \( \mathcal{M} \) and \( \mathcal{N} \) are subsets of \( \mathcal{M} \vee \mathcal{N} \), we have to have all of \(\{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \}\).
That was the easier direction. Now we have to show that that is all we need.
We showed in an earlier entry that for two subgroups \(M\) and \(N\) (of a group \( G \)) we have \( M \vee N = MN \) whenever \( M \leq N_{G}(M) \). I.e. that when \(M\) is a subgroup of the normalizer of \(N\). This is guaranteed to happen whenever \(G\) is Abelian, because every subgroup is normal. Thus
$$ \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} $$
is the join of the additive group of \( \mathcal{M} \) and \( \mathcal{N} \) (because \( MN \) means the same things as “\( M + N \)” when the binary operation is written additively, which is the case for the \(+\) operation of a module).
Finally, we have to show that multiplication by elements in \(R\) doesn’t add anything more.
Let \( w \) be an arbitrary element of \( \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} \), and \(r \) be an arbitrary element of \(R\). Then we have
\[\ rw = r(x + y) \]
where \(x \in \mathcal{M}\) and \( y \in \mathcal{N}\). This is an element of \( \mathcal{M} \vee \mathcal{N} \), a module (by definition), so we have to have
\[ r(x+y) = rx + ry \]
and, since \( \mathcal{M} \) is a module over \(R\), we must have \( rx \in \mathcal{M}\). Similarly, \(ry\) have to belong to \(\mathcal{N}\). So that means that
\[ rw \in \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \}\]
A nearly identical argument shows that \[ wr \in \{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} \]
Therefore,
$$ \begin{align} &\mathcal{M} \vee \mathcal{N} \subseteq \\ &\{ x + y | x \in \mathcal{M}, y \in \mathcal{N} \} \end{align} $$
Therefore, (18) holds.
QED
When we add more structure to a module, we might lose modularity. We’ll show that later, but first we’ll discuss a very basic example of a ring.
We’re all familiar with \(\mathbb{Z}\), the set of all integers, where \( m + n\) is the usual addition operator and \(mn\) multiplication. Since \( mn = nm\) for all \(m, n \in \mathbb{Z}\), it is a commutative ring, which we defined in the previous entry. However, it has another useful property which we have not discussed so far, but will do so now.
In order for \(mn = 0\) to hold in \( \mathbb{Z} \), either \(m = 0\), \(n=0\), or they both have to equal \(0\). This isn’t alway the case with rings, though. For rings, like \(\mathbb{Z}\), where it does hold, we call that ring an integral domain.
Definition: Integral Domain
Let \(R\) be a ring where for any two \(r_1\) and \(r_2 \in R\), we have $$ \begin{align} & r_1r_2 = 0 \implies \\ & r_1 = 0 \text{ or } r_2 = 0 \end{align} $$
then \(R\) is said to be an integral domain.
Now we’re going to fill in a gap we left in the previous entry. In that entry we showed that Ideals, i.e. Kernels of ring homomorphisms, are sub-rings. Now we’re going to see when a given sub-ring is an ideal, but first we need a definition
Definition: mod an Ideal
Let \( \phi : R \rightarrow S\) be a ring homomorphism from \(R\) to \(S\), and let \( I \) be the kernel of \(\phi\). Then, for any elements, \(r, s \in R\), we define
\[ r \equiv s \text{ (mod } I \text{)} \tag{19}\label{19} \]
if and only if (iff)
\[ \phi(r - s) = 0 \tag{20}\label{20} \]
What this means is that the addition operator of \(R\) determines the cosets of \(I\). Because of this, we know from our work with normal subgroups that these cosets will be well-behaved with respect to the addition operator. Next we’ll show that they are also well-behaved with respect to the multiplication operator.
Lemma: R mod I is a ring
Let \( \phi: R \rightarrow S \) be a ring homomorphism from a ring \(R\) to a ring \(S\). Let \(I\) be the kernel of \(\phi\). Then
\[ R / I := \{ [r] | r \in R \} \tag{21}\label{21} \]
is a ring, where
\[ [r] := \{ r’ \in R | r’ \equiv r \text{ (mod} I \text{)} \tag{22}\label{22} \} \]
Proof
We know that \(I\) is a subgroup of the group with the elements of \(R\) under the operator \(+\). We also know that it is a normal subgroup, since \(R\) with the addition operator is Abelian. Therefore \(R/I\) satisfies conditions 1.1, 1.2, 1.3, and 1.4 of the ring axioms from this theorem from group theory).
We also know from the proof of that theorem that for all \(x, y \in R\), \([x] + [y] = [x+y]\).
Next we’ll show that for all \(x, y \in R\), we also have
\[ [x][y] = [xy] \tag{23}\label{23} \]
To show this, suppose that \(x_1, x_2 \in [x]\), and \(y_1, y_2 \in [y]\). We want to show that \( [x_1y_1] = [x_2y_2] \). (This is similar to, but slightly different from what we did here)
\( \phi(x_1 - x_2) = 0 \) implies \(\phi(x_1) = \phi(x_2)\). Similarly, we have \( \phi(y_1) = \phi(y_2) \). Combining those two equalities, we get
\[ \phi(x_1)\phi(y_1) = \phi(x_2)\phi(y_2) \tag{24}\label{24} \]
and since \(\phi\) is a homomorphism, equation (24) means that
\[ \phi(x_1y_1) = \phi(x_2y_2) \]
and that means that
\[ \phi(x_1y_1 - x_2y_2) = 0 \]
thus \( [x_1y_1] = [x_2y_2] \), as we wanted, and equation (23) holds.
Equation (23) implies that
$$\begin{align} & ([ x ][ y ])[ z ] \\ &= ([ xy ])[ z ] \\ &= [ (xy)z ] \\ &= [ (x(yz)) ] \\ &= [ x ]([ yz ]) \\ &= [ x ]([ y ][ z ]) \\ \end{align}$$
which means that \(R/I\) satisfies condition 2 of the ring axioms.
We’ll show how to get condition 3.1, and the proof of 3.2 is very similar.
$$\begin{align} & [ x ]( [ y ] + [ z ] ) \\ &= [ x ]( [ y + z] ) \\ &= [ x (y + z) ] \\ &= [ xy + xz ] \\ &= [ xy ] + [ xz ] \\ \end{align}$$
Next, if condition 4 holds in \(R\), so we have \(1 \in R\), then $$\begin{align} & [ 1 ][ x ] \\ &= [ 1x ] \\ &= [x] \\ \end{align}$$
so condition 4 holds in \(R / I\). Finally, if condition 5 holds in \(R\), then
$$\begin{align} &[ x ] [ y ] \\ &= [ xy ] \\ &= [ yx ] \\ &= [ y ] [ x ] \\ \end{align}$$
so condition 5 holds in \(R/I\).
QED
Theorem: When a sub-ring is an Ideal
Let \(I\) be a sub-ring of a ring \(R\), such that for all \(r \in R\) we have
- \( rI \subseteq I \)
- \( Ir \subseteq I \)
Then \(I\) is an ideal of \(R\).
Proof
It makes sense that both of the conditions would have to hold for \(I\) to be the kernel of a ring homomorphism (sorry, this is not true! 1), because \(\phi(I) = 0\). The interesting fact is that these conditions are sufficient for \(I\) to be the kernel of a homomorphism.
We’ll do this by showing that \( \phi(r) = r + I \) is a homomorphism.
We should be very careful when using notation like this. We’re considering \(I\) to be a subgroup of the group of \(R\) with the binary operator \(+\). \(r + I\) is the coset of \(I\) containing \(r\).
So, by construction we know that \( \phi(x + y) = \phi(x) + \phi(y) \). The real work involves showing that \( \phi(xy) = \phi(x)\phi(y) \).
Let \(x, y \in R\), then
$$\begin{align} \phi(x) &= x + I \\ \phi(y) &= y + I \\ \end{align}$$
Let’s see what happens when we multiply the two cosets.When we do that we get
\( (x + I)(y + I) =\)\( xy\)\(+ xI \)\(+ Iy\)\(+ II \). By conditions 1 and 2 of the theorem, we know that \(xI\), and \(Iy \subseteq I\). Applying 1 repeatedly to every element of \(I\), we get that \(II \subseteq I\). That means that the product is a subset of \(xy + I\). It might not be all of \(xy + I\), but that doesn’t matter. We have just shown that \( \phi(x)\phi(y) \) will always lie within the coset \( xy + I \). So when we assign \( \phi(x)\phi(y) \) to a coset of \(I\), it must be assigned to \( xy + I \), which means that
\[ \phi(x)\phi(y) = \phi(xy) \]
Thus \( \phi \) is a ring homomorphism.
QED
That’s all we have for this entry. There’s quite a lot of material to go over yet. We’re just getting started with rings and fields. There will be more to come!
Thanks for reading!
-
This is only true for two-sided ideals. When \(R\) is non-commutative, it’s possible to have a subring which is a “left kernel”, but not a “right kernel or vice versa. ↩︎
