Partial Orders Lattices and Some Subgroups

In this article we mostly talk about partial orders, and lattices, which are a special type of partial order. We tie it in with our discussions of subgroups before proving two distribution laws for lattices.

Definition (partial order)

When writing out the partial order, we sometimes write it as an ordered pair \( (S, \leq)\), writing out the set and the partial order symbol.

As the name suggests, partial orders are less strict than total orders, like \( \leq \) among the rational numbers. For example, if we take \( \mathbb{Q} \times \mathbb{Q} \) with the relation \( (x_1, x_2) \leq (y_1, y_2) \) if and only if \( x_1 \leq y_1\) and \( x_2 = y_2 \), then this is a partial order. We can see that all of the axioms are satisfied by this order, but there are many ordered pairs which can’t be compared with each other. For example, \( (1, 2) \) and \( (2, 1 )\) aren’t comparable as \(x_2 \neq y_2 \).

Consider a second example of ordered pairs of rationals where \( (x_1, x_2 ) \leq (y_1, y_2 ) \) if and only if \( x_1 \leq y_1\) and \(x_2 \leq y_2\). Notice that with this partial order on \( \mathbb{Q} \times \mathbb{Q} \), that for any pair of elements \( x\) and \(y\), we can find a \(z\), such that \( x \leq z\) and \( y \leq z\). To see this, let \( (x_1, x_2)\) and \( (y_1, y_2) \) be two ordered pairs of rational numbers. Then if we let \( z = ( \max(x_1, y_1), \max(x_2, y_2) ) \), we see that \( x \leq z\) and \( y \leq z\) as we wanted. Similarly, by taking \( z = ( \min(x_1, y_1), \min(x_2, y_2) ) \), we have \( z \leq x\) and \( z \leq y\).

However, the first example we gave didn’t have this property. To see that, consider the example pair we gave above, \( x = (1,2)\) and \(y = (2,1) \). There is no \(z\) which can be comparable to both \(x\) and \(y\), because in that case \( z_2\), the second component of \(z\), would have to equal both \(1\) and \(2\).

This brings us to our next few definitions.

Definition (lattice)

Definition (join)

This is also called \( \max(x,y) \), which I used earlier when constructing the max of two ordered pairs. Hopefully that wasn’t too confusing, though, since I was using it in its more common setting, where the order is the usual order on the rationals. It can also be called the supremum of the set \( \{x, y\}\). We’ll define that more precisely later.

Definition (meet)

More precisely, \( x \vee y = z\), where \( \forall u, x \leq u\) and \( y \leq u \) implies \( z \leq u\). The precise definition for \( \wedge\) is similar. It is sometimes called \( \min(x,y)\).

Notice that \( \vee\) and \( \wedge \) are functions which map every element of \( S \times S\) to another element of \(S\), whenever \( (S, \leq) \) is a lattice. Now we prove that it’s associative.

Definition ( >= )

Hopefully that last definition didn’t confuse or surprise anyone.

Theorem ( v is associative):

Proof

Let \( s := x \vee y \), and \( t := y \vee z\). Also let \( a := s \vee z \) and \( b: = x \vee t \). Then we have

\[ a = s \vee z \]

\[ b = x \vee t \]

Then, by definition, we have \( a \geq z \), \(s \geq y\), and \( a \geq s\). By the transitivity of \( \geq\), we have \( a \geq y\). Therefore, by the definition of \(t\), we have \( a \geq t\). We also have \( s \geq x\), which means that applying transitivity again, \( a \geq x\). This means, that, by the definition of \(b\), \( a \geq b\). A similar argument will show that \(b \geq a\), and thus \( a = b\) by partial order axiom 2.

QED

Theorem ( ^ is associative)

Proof

Very similar to the proof for \( \vee \).

Definition (bounded lattice)

Theorem (subgroups form a bounded lattice)

Proof

By the definition of subgroup, we know that \( H_1 \leq H_2 \) and \(H_2 \leq H_3 \) implies \(H_1 \leq H_3\), so \( \leq \) is transitive. That takes care of partial order axiom 3. Axioms 1 and 2 are equally easy to prove. We also know that \( H \leq G \) and \( \{e \} \leq H\), for all \(H \in \mathcal{G}\), so it is bounded. The only thing that remains to be shown is that this partial order is a lattice. To do that we need to show that \( \vee \) and \( \wedge\) are well-defined. We’ll show that with a couple lemmas, which we’ll prove below.

Lemma (^ is well-defined)

Proof

Let \(a\) and \(b\) be in \(H_1 \cap H_2\), then \(a\) and \(b\) are in both \(H_1\) and \(H_2\), so by the subgroup test lemma, \(ab^{-1} \) in both \(H_1\) and \(H_2\), so their intersection must be a subgroup. Now, let \(K \) be any subgroup where \( K \leq H_1\) and \(K \leq H_2\). Then since \(K\) is a subgroup of both subgroups, it must also be a subset of both subgroups, so we must have \(K \leq H_1 \cap H_2\). This implies that \( H_1 \cap H_2 = H_1 \wedge H_2\).

QED

I’m starting to think I’ve already proved that the intersection of two subgroups is a subgroup, but at least the proof is very quick.

Lemma (v is well-defined):

Proof

\(G\) is in this intersection, so it is not an empty intersection. We’ve just shown that the intersection is a subgroup (in fact, in a previous entry, we showed that it’s true even for an infinite amount of subgroups). Clearly, any subgroup \( \geq\) to both \(H_1\) and \(H_2\) will contain this intersection, so it is \( \vee\).

QED

This completes our proof that subgroups form a bounded lattice.

Theorem (when v = *)

Proof

Clearly \(H \cdot N\) is a subgroup of \(G\) which contains both \(H\) and \(N\). Therefore, we only need to show that there is no strictly smaller subgroup which contains both. This is straight-forward.

Let \(K\) be a subgroup such that \( H \leq K \) and \(N \leq K\), then for any \(h \in H\), and any \( n \in N\), \(h \in K\) and \(n \in K\). Now, since \(K\) is a subgroup, \(hn \in K\). Therefore, \(H \cdot N \leq K\), thus \(H \cdot N = H \vee N\).

QED

Unfortunately, when \(H\) isn’t in the normalizer of \(N\), we don’t have this nice relationship.

I’ve mentioned before that what I’ve used as the definition for \(H \cdot N\) isn’t typical. It’s more common to define \( H \cdot N \), (also written simply as \(HN\), as \( \{ hn | h \in H, n \in N \} \). This definition is preferable when we don’t necessarily know that \(H\), and \(N\) are subgroups of a group \(G\), or when we’re not sure that \( H \leq N_{G}(N) \), because it is always equal to a subset of \(G\) (but not necessarily a subgroup of \(G\)). From now on, I’ll also use that as the definition of \(HN\), and treat the formula \( HN = \alpha^{-1} \circ \alpha(H) \) more like the result of a theorem, instead.

Theorem (HK = KH implies it is a subgroup)

Proof

Suppose \(HK = KH\), then let \(a = h_1k_1\) and \(b = h_2k_2\) be two elements of \(HK\). Then \(b^{-1} = k_2^{-1}h_2^{-1} \), so \(ab^{-1} = h_1 (k_1 k_2^{-1})h_2^{-1} \). Since \(K\) is a subgroup, \(k_1 k_2^{-1} = k_3 \), for some \(k_3 \in K\). Therefore the product is equal to \( (h_1 k_3) h_2^{-1}\). Now, since \(HK = KH \), \( h_1 k_3 \) is equal to \(k_4 h_4\), for some \(k_4 \in K\) and \(h_4 \in H\). Then the product is equal to \( k_4 (h_4 h_2^{-1})\), which itself is equal to \( k_4 h_5\), because \( h_4 h_2^{-1} = h_5\), for some \(h_5 \in H\), because \(H\) is a subgroup.

Therefore, \(ab^{-1} = k_4 h_5 \in KH\), which is equal to \(HK\), by assumption, and so by the subgroup test, \(HK \) is a subgroup.

QED

The argument in the proof that \(\vee = \cdot\) above still works here. Thus in this case as well we have \(HK = H \vee K\).

Next, we’re going to introduce

Definition (modular lattice)

To better appreciate that definition, here’s a picture of a lattice that is not modular.

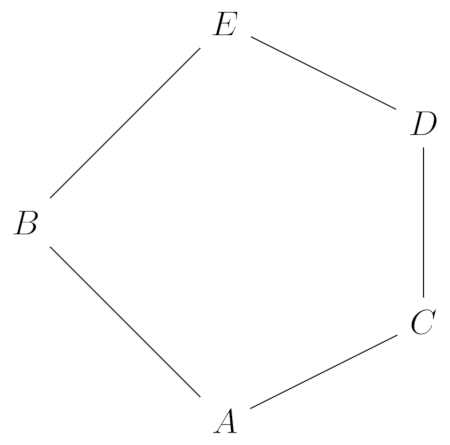
Notice that \((C \vee B) \wedge D = E \wedge D = D\), whereas \( (D \wedge B) \vee C = C \vee C = C\). Therefore, if \(C \neq D\), then the lattice is not modular. You can see that if this lattice were modular, that \(D = C\), so we would not have this pentagon appear without lines inside it. It would instead be a diamond.

It turns out that modular lattices behave fairly nicely.

Theorem (distribution I)

Proof

Notice that \(X \leq (X \vee Y) \), and \( X \leq (X \vee Z)\). We also have, \( (Y \wedge Z) \leq Y \leq (X \vee Y)\), so \( (Y \wedge Z) \leq (X \vee Y) \). Similarly, \( (Y \wedge Z) \leq Z \leq (X \vee Z)\), so combining these gives us

$$ \begin{align} &X \vee (Y \wedge Z) \\ &\leq (X \vee Y) \wedge (X \vee Z) \\ \end{align} $$

So, now we’re left with a sublattice that looks like this

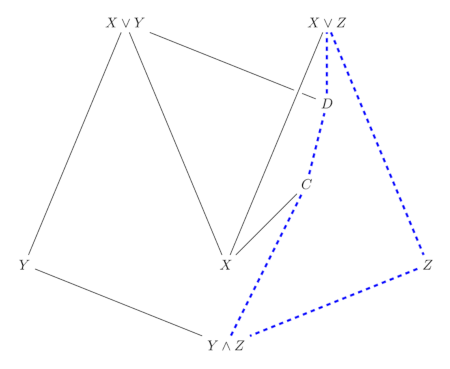
Where

$$ \begin{align} D &= (X \vee Y) \wedge (X \vee Z) \\ C &= X \vee (Y \wedge Z) \\ \end{align} $$

You can see that if the lattice is modular, then, as we showed above, the dashed pentagon cannot occur, so in that case \(D = C\), and we have equality.

QED

The final theorem for this entry will be the dual to the distributive result above.

Theorem (distribution II)

Proof

We have \( (X \wedge Y) \leq X \), and \( (X \wedge Y) \leq Y \leq (Y \vee Z) \), so \( (X \wedge Y) \leq X \wedge (Y \vee Z) \). Similarly, \( (X \wedge Z ) \leq X \wedge (Y \vee Z) \). Therefore, combining the two inequalities, we get

$$ \begin{align} &(X \wedge Y) \vee (X \wedge Z) \\ &\leq X \wedge (Y \vee Z) \\ \end{align} $$

If the inequality is strict, we end up with the following sublattice

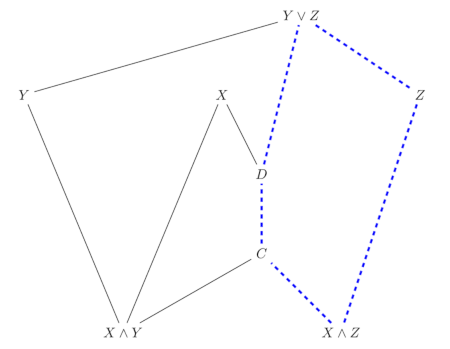
Where \(C = (X \wedge Y) \vee (X \wedge Z) \), and \(D = X \wedge (Y \vee Z)\). This results in a pentagonal sublattice with no interior lines (because there are no interior relations among the five elements of the lattice). This cannot happen in a modular lattice, so we must have \(C = D\) if \(\mathcal{L}\) is modular.

QED

These results might lure you into thinking that we can always get away with swapping \( \vee \) with \( \wedge\) as long as we swap “\( \leq\)” with “\( \geq\)”, but that isn’t always the case with lattices. As an example, consider the following lattice

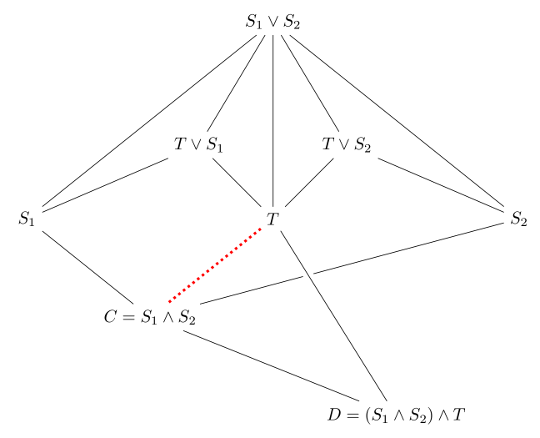
Notice that if \(C \neq D\), then \(T \leq S_1 \vee S_2\), however, \( T \not\geq S_1 \wedge S_2\). We’ll continue this discussion in a later entry…