Spheres, Distances, Maps and More!

Interactive Map

Note: The green line is fit by minimizing the \(L^2\) norm, and the blue line is fit by minimizing the \(L^{\infty}\) norm.

Introduction

In this entry, we use the dot product, which we first introduced in this entry, alongside some Linear Algebra and Geometry to figure out how to draw a line between two points on a sphere. We also derive a formula for calculating the distance between two points as well as the distance from a point to a line on a sphere.

Notation Used in this Entry

Notation varies among fields and we make no effort to conform to any particular one of them. If you’re an astronomer, physicist, etc… we apologize for the inconvenience this may cause.

1. \(\theta\) is the longitude.
2. \(r\) is the radius of the sphere.
3. \(\phi\) is the latitude.

When we give coordinates in the Cartesian coordinate system, you are free to envision it however you like. We will convert between them like this

Converting between polar and Cartesian coordinates

Going from polar to Cartesian, we use

$$\begin{align} x &= r \cos{\theta}\cos{\phi} \\ y &= r \sin{\theta}\cos{\phi} \tag{1}\label{1} \\ z &= r \sin{\phi} \end{align}$$

while going the other way, from Cartesian to polar, we use

$$\begin{align} r &= \sqrt{x^2 + y^2 + z^2} \\ \phi &= \sin^{-1}(\frac{z}{r}) \tag{2}\label{2}\\\ \theta &= \sin^{-1}(\frac{y}{r \cos{\phi}}) \end{align}$$

A little caution is required when using (2). If \( \langle x, y, z \rangle = \vec{0}\), then \(r = 0\), and it doesn’t matter what \( \phi \) and \( \theta\) are. Notice also that if we are at either pole, so that \(\phi = \pm \frac{\pi}{2}\), then \(\theta\) doesn’t matter, which is good, because it can’t be determined, since the \(\cos{\phi}\) in the denominator is equal to \(0\).

Distance between two points on a sphere

Notice here that we want the distance as you would travel on the surface of the sphere to get from one point to another. Further, notice that this distance will never be greater than \( \pi \cdot r\), because that is equal to half of the circumference of the sphere. If you find yourself traveling more than \(\pi \cdot r\) to reach your destination, you should have headed in the opposite direction.

Let \(p_1\) and \(p_2\) be two distinct points on a sphere. We can think of both of them as vectors with length (or norm) \(r\), the radius of the sphere. When we think of them as vectors, we can denote them as \(\vec{p_1}\) and \(\vec{p_2}\) to make that clearer.

Recall from An Intro to the Dot Product that the dot product of \(\vec{p_1}\) and \(\vec{p_2}\) is equal to the cosine of the angle between them multiplied by both of their norms. I.e. if \(\alpha\) is the angle between \(\vec{p_1}\) and \(\vec{p_2}\), then

\[ ||\vec{p_1}|| || \vec{p_2}|| \cos({\alpha}) = \vec{p_1} \cdot \vec{p_2} \tag{3}\label{3} \]

We can use this to calculate \(\alpha\)

\[ \alpha = \cos^{-1}({ \frac{ \vec{p_1} \cdot \vec{p_2} }{ || \vec{p_1} || || \vec{p_2} || } }) \tag{4}\label{4} \]

Since \(p_1\) and \(p_2\) lie on the surface of a sphere of radius \(r\), both of the norms are equal to \(r\). Now, once we have the angle \(\alpha\) we can calculate the arc length between the points \(p_1\) and \(p_2\) as \(\alpha r\).

This makes sense, because if \(\alpha = 2\pi\), so we’re going completely around the sphere, we would travel the entire length of the circumference of a circle with radius \(r\) – i.e. \(2\pi r\).

The distance, then, is given by

\[ d(p_1, p_2) = r \cos^{-1}({\frac{\vec{p_1} \cdot \vec{p_2}}{r^2}}) \tag{5}\label{5}\]

since \(|| \vec{p_i} || = r \).

When we want to calculate the distance between two points on a globe, they’ll probably be specified with latitude and longitude (and the radius of the sphere). We can use the equations in (1) above to determine the \(\vec{p_i}\).

Let \(p_i = \langle \phi_i, \theta_i \rangle \), and \(r\) be the radius of the sphere. Then

\[ \vec{p_i} = \langle x_i, y_i, z_i \rangle \tag{6}\label{6} \]

where

$$\begin{align} x_i &= r\cos(\theta_i)\cos(\phi_i) \\ y_i &= r\sin(\theta_i)\cos(\phi_i) \tag{7}\label{7} \\ z_i &= r\sin(\phi_i) \end{align}$$

Combining (7) with (5) gives us

\[ d(\langle \phi_1, \theta_1 \rangle, \langle \phi_2, \theta_2 \rangle) = r \cos^{-1}( \gamma )\]

where (after rearranging some of the terms)

$$\begin{align} \gamma = & \cos(\phi_1)\cos(\phi_2)\cos(\theta_1)\cos(\theta_2) \\ + & \cos(\phi_1)\cos(\phi_2)\sin(\theta_1)\sin(\theta_2) \tag{8}\label{8}\\ + & \sin(\phi_1)\sin(\phi_2) \end{align}$$

Drawing a line between two points on a sphere

Even on a sphere, the rule that a line is determined by two distinct points holds. Notice that a line on a sphere will wrap around onto itself, once it has finished going completely around the sphere. When it does this it forms a great circle.

That great circle is the intersection of a 2-dimensional plane and the sphere. The plane goes through the center of the sphere, which our construction has at \( (0,0,0) \).

To see that this is true, represent the two points as vectors \(\vec{p_1}\) and \( \vec{p_2} \). That plane is then the span of \(\vec{p_1}\) and \(p_2\), where

\[ \text{Span}(\{ \vec{p_1}, \vec{p_2} \}) := \{ a_1\vec{p_1} + a_2\vec{p_2} | a_1, a_2 \in \mathbb{R} \} \tag{9}\label{9} \]

There is a subtlety we have to watch out for. We need to make sure that this span is 2-dimensional. It could be 1-dimensional. Even though we assumed that \(p_1\) and \(p_2\) are distinct points on the surface of the sphere, if they are at opposite ends of the sphere (e.g. the north and the south poles), then \(\vec{p_1} = - \vec{p_2}\), so we have \(\text{Span}(\{\vec{p_1}, \vec{p_2}\}) = \text{Span}(\{ \vec{p_1} \})\), which obviously has dimension 1 (and not 0, because \(r >0\), so \(\vec{p_1} \neq \vec{0}\)).

In the above case where \(\vec{p_1} = -\vec{p_2}\), there are an infinite number of possible planes we can use. This is because there are an infinite number of great circles that contain both \(p_1\) and \(p_2\). Pick any third point, \(p_3\), on the surface of the sphere which is not equal to either \(p_1\) or \(p_2\). The great circle containing both \(p_1\) and \(p_3\) will also contain \(p_2\). This is because every great circle which contains a point \(q\) will also contain the point on the opposite side of the sphere to \(q\).

Now we’ll see how to find the plane and with that, find the great circle.

Definition (cross product)

Notice that

$$\begin{align} \vec{p} \times \vec{q} &= -\vec{q} \times \vec{p} \\ \vec{p} \cdot ( \vec{p} \times \vec{q} ) &= 0 \tag{12}\label{12}\\ \vec{q} \cdot (\vec{p} \times \vec{q}) &= 0
\end{align}$$

We also have for any \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) \() \in \mathbb{R}^3 \)

$$\begin{align} &\vec{u} \times (a\vec{v} + b\vec{w}) = \tag{13}\label{13} \\ &a(\vec{u} \times \vec{v}) + b(\vec{u} \times \vec{w}) \end{align}$$

Verifying (12) and (13) is straight-forward. All you have to do is plug in (11) and recall the definition of the dot product (for 12).

Theorem (perpendicular vector determines 2-d plane through the origin)

Proof

A 2-dimensional plane \(P\) is a 2-dimensional subspace of \(\mathbb{R}^3\), so it is equal to \( \text{Span}(\{ \vec{u}, \vec{v} \}) \), where \( \vec{u} \neq a \vec{v}\) for any \(a \in \mathbb{R}\). I.e. it is the span of two linearly-independent vectors.

Let \(\vec{p} = \vec{u} \times \vec{v} \). Let \(\vec{w} \in P\), then we have \(\vec{w} = a\vec{u} + b\vec{v}\), which means that \( \vec{p} \cdot \vec{w} = \vec{p} \cdot ( a\vec{u} + b\vec{v} ) \), and since the dot product distributes (you can easily verify this) that dot product is equal to \(a \vec{p} \cdot \vec{u} + b \vec{p} \cdot \vec{v}\). This is equal to \( a(\vec{u} \times \vec{v}) \cdot \vec{u} + b(\vec{u} \times \vec{v}) \cdot \vec{v} \), which by (12) above, we see is equal to \(0\). Thus \(\vec{p}\) satisfies part 1 of the lemma.

The proof of part 2 of the lemma is much more work. In it, we make frequent use of the transpose of a vector (and also of a matrix). The transpose of a row vector is a column vector and vice versa. Similarly, the transpose of an \( n \times m\) matrix is an \(m \times n \) matrix, where the rows from the original are the columns in the transpose.

Notice what happens to the subscripts

$${\begin{pmatrix} a_{1,1} & a_{1,2} & … & a_{1, m} \\ a_{2,1} & a_{2,2} & … & a_{2, m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n, 2} & … & a_{n, m} \\ \end{pmatrix}}^{T}=\begin{pmatrix} a_{1,1} & a_{2,1} & … & a_{n, 1} \\ a_{1,2} & a_{2,2} & … & a_{n, 2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1,m} & a_{2,m} & … & a_{n,m} \\ \end{pmatrix}$$

To start the proof of part 2, notice that if \(\vec{u} = \langle u_1, u_2, u_3 \rangle\) and \(\vec{v} = \langle v_1, v_2, v_3 \rangle\), and \( \vec{q} = \langle q_1, q_2, q_3 \rangle\), then we have the following matrix equations

$$\begin{pmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ \tag{14}\label{14} p_3 \\ \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix}$$

and

$$\begin{pmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} q_1 \\ q_2 \\ \tag{15}\label{15} q_3 \\ \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix}$$

Let’s denote the matrix on the left as \(M\), so

$$M=\begin{pmatrix} u_1 & u_2 & u_3 \\ v_2 & v_2 & v_3 \\ 0 & 0 & 0 \\ \end{pmatrix}$$

Let \(\vec{x} \in \text{Ker}(M) \cap P \), the intersection of the kernel of \(M\) and \(P\). Since \( \vec{x} \in P\), we have \( \vec{x} = a\vec{u} + b\vec{v}\), which means

$$\vec{x}=\begin{pmatrix} u_1 & v_1 & 0 \\ u_2 & v_2 & 0 \\ u_3 & v_3 & 0 \\ \end{pmatrix}\begin{pmatrix} a \\ b \tag{15.1}\label{15.1}\\ c \\ \end{pmatrix}$$

where \(c\) can be any real number. If we let \( {\vec{y} = \langle a, b, c \rangle}^{T}\), then

\[ \vec{x} = M^{T}\vec{y} \]

However, since \( \vec{x} \in \text{Ker}(M)\), we also have

\[ M\vec{x} = \vec{0} \]

combining them and computing the norm squared of \(\vec{x}\), we get

$$\begin{align} \vec{x} \cdot \vec{x} &= \vec{x}^{T} \vec{x} \\ &= (\vec{y}^{T}M)(M^{T}\vec{y}) \\ &= \vec{y}^{T}(MM^{T}\vec{y}) \tag{16}\label{16}\\ &= \vec{y}^{T}(M\vec{x}) \\ &= \vec{y}^{T} \vec{0} \\ &= 0 \end{align}$$

So the intersection of \( \text{Ker}(M) \) and \(P\) is \( \{ \vec{0} \} \).

We’ll leave it to the reader to show that both \(P\) and \(\text{Ker}(M)\) are subspaces of \(\mathbb{R}^3\).

Finally, let \( \mathcal{B}_1 = \{ \vec{\beta_1}, \vec{\beta_2}, … , \vec{\beta_k} \} \) be a basis for \(P\) and \( \mathcal{B}_2 = \{\vec{\gamma_1}, \vec{\gamma_2}, … , \vec{\gamma_l} \} \) be a basis for \( \text{Ker}(M) \). Then \( \mathcal{B}_1 \cup \mathcal{B}_2\) is still a basis. It is a basis for a \(k + l\) dimensional subspace of \( \mathbb{R}^3 \). To see this, suppose

$$\begin{align} \vec{0} &= \vec{v_1} + \vec{v_2} \\ \vec{v_1} &= b_1\vec{\beta_1} + … + b_k\vec{\beta_k} \tag{17.1}\label{17.1}\\ \vec{v_2} &= g_1\vec{\gamma_1} + … + g_l\vec{\gamma_l} \tag{17.2}\label{17.2} \end{align}$$

then \( \vec{v_1} = -\vec{v_2} \), which means by (17.1) and (17.2) that \(\vec{v_1} \in \text{Ker}(M) \cap P \). By (16), this means that \(\vec{v_1} = \vec{0}\). Similarly, \(\vec{v_2} = \vec{0}\), and since \(\mathcal{B}_1\) and \(\mathcal{B}_2\) are both bases, this means that \(b_i = 0\) and \(g_i = 0\). Therefore \( \mathcal{B}_1 \cup \mathcal{B}_2 \) is a basis.

Putting everything together, we have shown that the dimension of \(P\) + the dimension of \( \text{Ker}(M) \) must be less than the dimension of \(\mathbb{R}^3\), which is 3 (by definition). Since \(\dim{P} = 2\), we must have \( \dim(\text{Ker}(M)) \leq 1 \).

Now, since \( \vec{p} = \vec{u} \times \vec{v} \) is a non-zero element of \( \text{Ker}(M) \) it must have dimension at least 1. This means that \( \text{Ker}(M) = \{a\vec{p} | a \in \mathbb{R}\} \).

By (15.1) this gives us our result. This finishes the proof of part 2 of this lemma.

QED

Now, back to drawing a line connecting two points on a sphere.

By the above theorem, if we let \(\vec{p_1}\) and \(\vec{p_2}\) represent the two points as vectors, then the plane spanned by the two is equal to the set of \(\vec{w} \in \mathbb{R}^3\), such that \(\vec{w} \cdot (\vec{p_1} \times \vec{p_2}) = 0\). That means that the great circle that passes through \(p_1\) and \(p_2\) is the subset of that plane whose vectors have length equal to \(r\), the radius of the sphere. Let

\[ \vec{n} := \vec{p_1} \times \vec{p_2} \tag{18}\label{18}\]

This means that the great circle which passes through \(p_1\) and \(p_2\) is equal to

\[ \{ \vec{w} \in \mathbb{R}^3 | \vec{w} \cdot \vec{n} = 0, || \vec{w} || = r \} \tag{19}\label{19} \]

We can use this to determine the distance between a third point, \(u\) and the this great circle. Let \(\vec{u}\) represent \(u\) as a vector. Then in order to find the distance to the great circle, we have to determine the angle that \(\vec{u}\) makes with the plane that defines the great circle. We can find that angle by first projecting \(\vec{u}\) on to the plane.

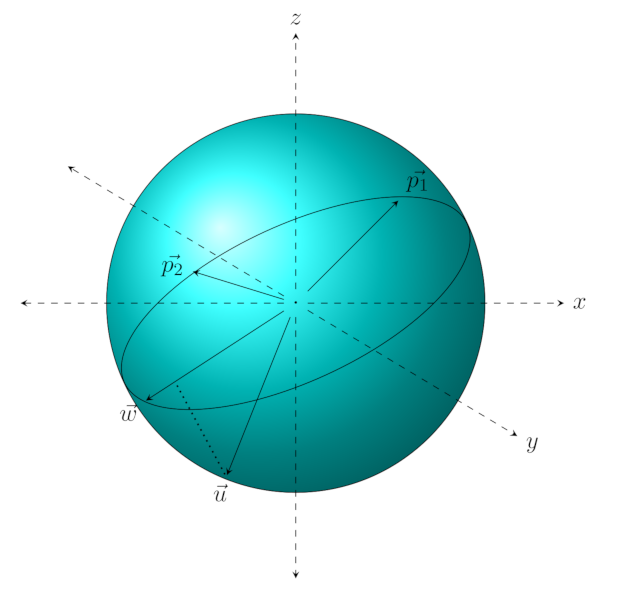
Notice the dotted line from \(\vec{u}\) to the plane of the great circle. That line is obtained by adding \( \lambda \vec{n}\), the perpendicular (or “normal”) vector to the plane, until we meet the plane.

That happens exactly when we find the \(\lambda\), such that

\[ (\vec{u} + \lambda \vec{n}) \cdot \vec{n} = 0 \tag{20}\label{20} \]

which implies that

\[ \lambda = -\frac{\vec{u}\cdot\vec{n}}{\vec{n}\cdot\vec{n}} \tag{21}\label{21}\]

this means that

\[ \vec{w} = r\frac{ \vec{u} - (\frac{\vec{u}\cdot\vec{n}}{\vec{n}\cdot\vec{n}}) \vec{n} }{ || \vec{u} - (\frac{\vec{u}\cdot\vec{n}}{\vec{n}\cdot\vec{n}}) \vec{n} || } \tag{22}\label{22} \]

Therefore, the distance that we travel on the surface of the sphere is determined by applying (22) to the distance formula we derived above in equation (4).

When we apply that, we get

Distance between a point on a sphere and a line on the sphere

$$\begin{align} \vec{u} \cdot \vec{u} &= r^2 \\ \mu &= \vec{u} \cdot \vec{n} \\ \nu &= \vec{n} \cdot \vec{n} \\ d(\vec{u}, \vec{w}) &= r\cos^{-1}(\frac{\vec{u}\cdot\vec{w}}{||\vec{u}|| || \vec{w}||}) \tag{23}\label{23} \\ \end{align}$$

The first line is simply because \(\vec{u}\) is the vector to a point on the sphere, and the sphere has radius \(r\).

With the map at the top of the page, we’ve added the ability to fit a line to two or more points on the map by using the distance formula given by equation (23). We calculate the total distance of all of the given points to a line, and then use gradient descent to try to minimize that function.

In fact, we don’t start with gradient descent. We calculate the distance for 10,000 different great circles (which correspond to 10,000 different \(\vec{n}\)’s). We take the \(\vec{n}\) whose great circle is nearest to all of the provided points, and then use gradient descent to get an even better result.

If you provide exactly two points, then it just calculates \(\vec{n}\) as the cross product of the two vectors representing those points. That line will fit exactly.

Computing latitude from longitude and a perpendicular vector

Lastly, once we have found a suitable \(\vec{n}\) whose great circle minimizes distances to the given points, we have to calculate a latitude for each longitude. This is so that we can compute the great circle as a function of longitude. This won’t work if the great circle is a line of longitude (and the line of longitude on the opposite side of the earth). This only happens, when \(\vec{n}\) lies on the \(xy\) plane, where \(z = 0\). If this happens, our great circle fitting function will fail. Sorry. Maybe one day we’ll address this corner case, but not today..

Since we only care about latitude and longitude, it’s much easier to ignore \(r\) by assuming it’s equal to 1. If \(\vec{n} = \vec{p_1} \times \vec{p_2}\), then let

\[ \vec{t} = \frac{\vec{n}}{|| \vec{n} ||} \tag{24}\label{24} \]

You can check for yourself that \(|| \vec{t} || = 1\).

We will write the components of \(\vec{t}\) as \( \langle t_1, t_2, t_3 \rangle \), and \(\langle x,y,z\rangle\) will represent a point on the great circle (which is orthogonal to \(\vec{t}\)). Then, by definition, we have \(\langle t_1, t_2, t_3\rangle \cdot \langle x,y,z\rangle = 0\). Since we’re assuming that \(\vec{t}\) does not lie on the equator, we have \(t_3 \neq 0\), so we can now safely solve for \(z\) in terms of \(x\) and \(y\). When we do that, we get

\[ z = -\frac{1}{t_3}(t_1x + t_2y) \tag{25}\label{25} \]

and since we’re trying to solve for latitude in terms of longitude, we’ll convert this to polar coordinates by applying equation (1) (from near the top of the page). When we do that, we get

\[ \sin(\phi) = -\frac{1}{t_3}[t_1\cos(\theta) + t_2\sin(\theta)]\cos(\phi) \tag{26}\label{26} \]

solving for \(\phi\) gives us

\[ \phi = \tan^{-1}(-\frac{t_1\cos(\theta) + t_2\sin(\theta)}{t_3}) \tag{27}\label{27}\]

Thank you

That’s all for this entry. There will be bugs and mistakes in this entry. We’ll try to update this page with fixes as they are pointed out to us (which we do with every entry).

A special thanks goes out to Open Street Map, which serves an open-source map of the world. It’s completely free to use! We also have to thank Leaflet. They provide an open-source javascript library, which you can use to create interactive maps!

While we’re at it, this site is currently hosted on GitHub pages for free! Free is great!

Thanks!!