The Sum of All Prime Reciprocals Is Infinite

Here we show the classic result that \( \sum\limits_{p \text{ is prime}} \frac{1}{p} = \infty \).

We’ll start with the much easier result that \( \sum\limits_{n=1}^{\infty} {\frac{1}{n}}= \infty \). We’ll have to use some calculus.

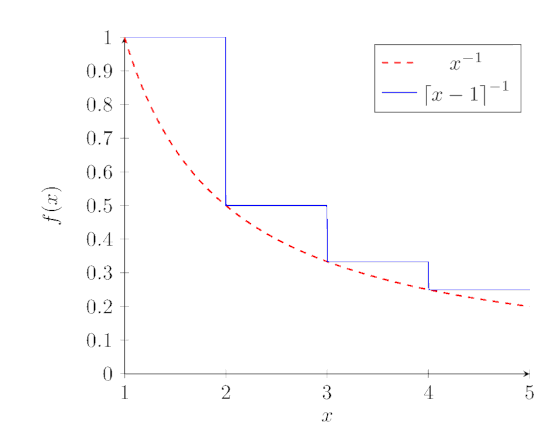
Let’s begin by considering the area under the solid blue line in the image above. The function is \( {\left \lceil{x - 1}\right \rceil}^{-1} \). Notice that the area under the curve from \( x = 1 \) to \( x = 2\) (i.e. \( \int_{1}^{2} { {\left \lceil{x - 1}\right \rceil}^{-1} dx } \) ) is just the area of a rectangle with height of 1 and a base of length 1 (note that the x and the y axes are not drawn to the same scale). I.e. the integral from \(1\) to \(2\) is \(1\). Similarly the integral from \(2\) to \(3\) is \(\frac{1}{2}\), the integral from \(3\) to \(4\) is \(\frac{1}{3}\) and so on. In this way, we see that \( \int_{1}^{n} { {\left \lceil{x - 1}\right \rceil}^{-1} }dx = \sum\limits_{k=1}^{n-1} {\frac{1}{k}} \), where \( n \geq 1\) Next we notice that \( {\left \lceil{x - 1}\right \rceil} \leq x \), so \( {\left \lceil{x - 1}\right \rceil}^{-1} \geq \frac{1}{x} \). This means that the area under the blue curve is greater than or equal to the area under the dotted red curve. I.e. \( \int_{1}^{n} { {\left \lceil{x - 1}\right \rceil}^{-1} dx} \geq \int_{1}^{n}{ \frac{1}{x} }dx \). This implies that \( \sum\limits_{k=1}^{n-1} {\frac{1}{k}} \geq \int_{1}^{n}{ \frac{1}{x} }dx \) In this article I’m not going to prove that \( \int_{1}^{n}{ \frac{1}{x} }dx = \ln(n) \), but it’s true. Maybe I’ll prove it later. This shows us that \( \sum\limits_{k=1}^{n-1} {\frac{1}{k}} \geq \ln(n) \). Since \( \ln(n) \) can be made arbitrarily large, so can the sum of the reciprocals of the integers.

QED

To prove that the sum of the reciprocals of the primes is infinite we’ll use a result similar to what we just got, but this time with the function \( \frac{1}{x\ln(x)}\). While it’s fresh in our minds, let’s get that lemma out of the way.

Lemma (a)

Proof

Similarly to what we did before, notice that

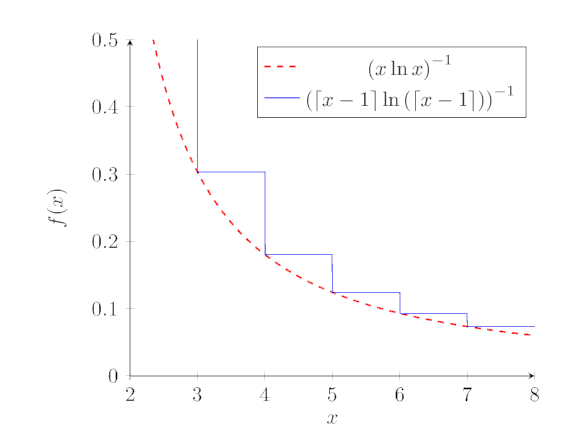
$$ \begin{align} &\sum\limits_{k=m}^{n-1} { \frac{1}{k\ln(k)} } = \\ &\int_{m}^{n} { ( \left \lceil x - 1 \right \rceil \ln ( \left \lceil x - 1 \right \rceil ) )^{-1} dx} \\ \end{align} $$

and, like before,

$$ \begin{align} &\left \lceil x - 1 \right \rceil \le x \Rightarrow \\ &( \left \lceil x - 1 \right \rceil \ln ( \left \lceil x - 1 \right \rceil ) )^{-1} \ge (x \ln(x))^{-1} \\ \end{align} $$

Combining the last two lines gets us

$$ \begin{align} &\sum\limits_{k=m}^{n-1} { \frac{1}{k\ln(k)} } \\ &\ge \int_{m}^{n} { (x \ln(x))^{-1} dx } \\ \end{align} $$

We can evaluate that integral by performing a u substitution with \( u = \ln(x) \). When we do that we get that the integral is equal to \( \ln ( \ln (n) ) - \ln (\ln (m) ) \). For any fixed m, when we evaluate the limit as n goes to infinity, we see that although it may get there slowly, \( \ln ( \ln (n) ) \) grows to infinity, and that was the last step in proving the lemma.

QED

Lemma (b)

Proof

Notice that at \( x = e^2\), we get \( \frac{ e^{2}} { \ln(e^{2}) } = \frac{e^{2}} {2} \ge \sqrt{ e^{2} } = e \). Now we’ll show that \( \frac{x} {\ln(x)} \) grows faster than \( \sqrt{x} \) by showing that the derivative of \( \frac{ (\frac{x} { \ln(x) }) }{ \sqrt{x} } \ge 1 \). Taking the derivative is just tedious calculus. The result (feel free to check it yourself) is \[ \frac{ (\frac{1}{2} \ln(x) - 1)x^{- \frac{1}{2}}} { \ln(x)^{2} } \] Notice that the denominator is squared, and non-zero when \( x > e^{2}\), while the numerator is the product of two terms which will both be positive for such \(x\).

QED

Now let’s do some actual number theory.

Lemma (c)

Proof

We’re going to assume that the natural numbers can be factored uniquely into powers of prime divisors. It’s true, and maybe I’ll write about it in another article. That result is known as the Fundamental Theorem of Arithmetic. A consequence of the Fundamental Theorem of Arithmetic is that for any natural number n, n can be factored into prime powers. That means that for any \( n \), there is a finite set \( \mathbb{P}_n := \{ p_1, p_2, p_3, …, p_k \} \) of primes that divide \( n \). If \( \mathbb{P}_n \) has only one number in it (i.e. \( | \mathbb{P}_n | = 1 \) ), then we say that \( n \) is a prime power. Because \( n = p^k \) for some \( p \) and some \( k \). Now let’s define \( \epsilon(p,n) := \max\limits_{k} \{p^k | n\} \). I.e. the maximum \(k \) such that \( p^k \) divides \( n\). We can then rewrite \(d \) and \( n\) as:

$$ \begin{align} d &= \prod\limits_{ p \in \mathbb{P}_d } p^{ \epsilon(p, d) } \\ n &= \prod\limits_{ p \in \mathbb{P}_n } p^{ \epsilon(p, n) } \\ \end{align} $$

By our assumption, we have \( \mathbb{P}_d \subseteq \mathbb{P}_n \) and for all \( p \in \mathbb{P}_d \), \( \epsilon(p, d) \leq \epsilon(p, n) \). Combining those two observations gives us

$$ \begin{align} n &= \prod\limits_{ p \in \mathbb{P}_n } p^{ \epsilon(p, n) } \\ &= \prod\limits_{ p \in \mathbb{P}_d } p^{ \epsilon(p, n) } \cdot \prod\limits_{ p \in \mathbb{P}_n \setminus \mathbb{P}_d } p^{ \epsilon(p, n) } \\ &= ( \prod\limits_{ p \in \mathbb{P}_d } p^{ \epsilon(p, d) } \cdot \prod\limits_{ p \in \mathbb{P}_d } p^{ \epsilon(p, n) - \epsilon(p, d)} ) \cdot \prod\limits_{ p \in \mathbb{P}_n \setminus \mathbb{P}_d } p^{ \epsilon(p, n) } \\ &= d \cdot \prod\limits_{ p \in \mathbb{P}_d } p^{ \epsilon(p, n) - \epsilon(p, d)} \cdot \prod\limits_{ p \in \mathbb{P}_n \setminus \mathbb{P}_d } p^{ \epsilon(p, n) } \\ \end{align} $$

QED

Lemma (d)

Proof

First notice that \( \Lambda(x) \) is \( e \) to the power of a sum of natural logarithms, so we can change that to the product \[ e^{\Lambda(x)} = \prod\limits_{ p^k \le n \textbf{ and } p \in \mathbb{P} } {p} \tag{1}\label{1} \] Next, let’s pick an arbitrary \( d \leq n \) and apply lemma (c) by considering one of its prime divisors, \( p \). Recall from the proof of lemma (c) that \( \epsilon(p, d) := \max\limits_{k} {p^k | n} \), and further notice that by definition \( p^{ \epsilon(p, d)} | d \), so \( p^{ \epsilon(p, d)} \leq d \leq n \). Since \( \epsilon(p,d) \) is the maximum \( k \), we can also see that for every \( k = 1, 2, 3, …, \epsilon(p, d) \), we have \( p^k | d \), and so \( p^k \leq d \leq n) \). Therefore by equation (1), \(p^{ k } | e^{ \Lambda(n) } \) whenever \( k \leq \epsilon(p,d) \), so with lemma (c) we are done with the proof of this lemma.

QED

Three Facts About an Integral

Proof of 1 and 2

Let \( f_{n}(x) := x^n(1-x)^n \), notice that for \( x \in (0, 1) \), \( f_{n}(x) \gneq 0 \), but \(f_{n}(x) = 0 \) at \( x = 0 \) and \( x = 1\). Also,

$$ \begin{align} &\frac{d}{dx} f_n(x) \\ = &n[ x^{n-1}(1-x)^{n-1}(x-1) - x^{n-1}(1-x)^{n-1}x ] \\ = &n[ f_{n-1}(x)(1-x) - f_{n-1}(x)x ] \\ = &nf_{n-1}(x)(1 - 2x) ] \\ \end{align} $$

So, for \( x \in (0, 1) \), the derivative is equal to 0 only at \( x = \frac{1}{2} \). Since \(f_{n}(1/2) = \frac{1}{2^{2n}} \) and \( 0 \) at \( x = 0\) and \( x = 1\), we conclude that \( x = \frac{1}{2} \) is a maximum of \(f_n) \). We just proved 2. By considering our derivative formula, we can also determine that since \( f_{n}(x) \) is increasing from \(0\) to \( \frac{1}{2} \) and decreasing from \( \frac{1}{2} \) to \(1\), and because \( f_{n}(1/4) = f_n(3/4) = \frac{1}{4^{2n}}\) that \( I_n \geq (\frac{3}{4} - \frac{1}{4}) \frac{1}{4^{2n}} \gneq 0 \). We just proved 1.

Proof of 3

Proving 3 is easy with the help of lemma (d). We can evaluate \( \int_0^1 x^n(1-x)^n dx \) by first expanding \( (1 - x)^n \) into a polynomial. The degree of that polynomial will be \( n \), so when you multiply it by \( x^n \), you end up with a polynomial of degree \( 2n \). Then, when you take the indefinite integral you end up with a polynomial with degree \( 2n + 1 \) where all the terms have denominators that are integers \( \leq 2n + 1 \). By lemma (d), when you multiply that polynomial by \( e^{\Lambda(2n+1)} \), you end up with a polynomial with integer coefficients. Therefore evaluating the definite integral will result in an integer value. This finishes the proof of 3.

QED

Now we’re getting somewhere. When we combine 1 and 3, we get that \( I_n \cdot e^{\Lambda(2n+1)} \geq 1 \). That gets us \( e^{\Lambda(2n+1)} \geq \frac{1}{I_n} \). Using 2 from above, we get \( e^{ \Lambda(2n+1) } \geq 4^{n} \). Taking the logarithm of both sides (which are both positive), we get \[ \Lambda(2n+1) \geq 2\ln(2)n \tag{2}\label{2} \] Now let’s define \( \pi(x) := | { p \in \mathbb{P} | p \leq x } |\).

Lemma (e)

Proof

By definition, \( \Lambda(n) = \sum\limits_{p^k \leq n} {\ln(p)} \). That’s equal to

$$ \begin{align} &\sum\limits_{ p \leq n } {( \sum\limits_{ k = 1 }^{ \max\limits_{ k } { p^k \leq n } } \ln(p) )} \\ = &\sum\limits_{ p \leq n } { \max\limits_{ k } { p^k \leq n } \cdot \ln(p) } \\ = &\sum\limits_{ p \leq n } { \ln(p ^{ \max\limits_{ k } { p^k \leq n } }) } \\ \leq &\sum\limits_{ p \leq n } { \ln(n) } = \pi(n) \cdot \ln(n) \\ \Rightarrow &\frac{ \Lambda(n) }{ \ln(n) } \leq \pi(n)\\ \end{align} $$

QED

If we combine that with equation (2) above, we get

$$ \begin{align} &\pi(2n+1) \geq \frac{2\ln(2)n}{ \ln(2n+1) } = \\ &\frac{\ln(2)(2n+1)}{\ln(2n+1)} - \frac{\ln(2)}{\ln(2n+1)}\tag{3}\label{3} \\ \end{align} $$

If \( p \geq 3 \), then \( p \) is odd, so we can replace \( 2n + 1 \) with \( p_k \) for some prime \( p_k \geq 3 \). This gives us

$$ \begin{align} k &= \pi(p_k) \\ &\geq \frac{\ln(2)p_k}{\ln(p_k)} - \frac{\ln(2)}{\ln(p_k)} \tag{4}\label{4} \\ \end{align} $$

Then, since \( p_k \geq 3 \), we get

$$ \begin{align} k &\geq \frac{ \ln(2) }{ 2 } \cdot \frac{ p_k } { \ln(p_k) } \tag{5}\label{5} \\ &\Rightarrow k \cdot \ln(p_k) \geq \frac{ \ln(2) }{ 2 } \cdot p_k \tag{6}\label{6} \\ \end{align} $$

By lemma (b), we see that

$$ \begin{align} &\frac{ \ln(2) }{ 2 } \cdot \frac{ p_k }{ \ln(p_k) } \\ \geq &\frac{ \ln(2) }{ 2 } \cdot \sqrt{p_k} \\ \end{align} $$

so if we combine that result with equation (5) and (6) above, we get

$$ \begin{align} &k \geq \frac{ \ln(2) }{ 2 } \cdot \sqrt{p_k} \\ \Rightarrow &k^2 \cdot ( \frac{ 2 }{ \ln(2) } )^2 \geq p_k \\ \Rightarrow &k \cdot \ln(k^2 \cdot ( \frac{ 2 }{ \ln(2) } )^2 ) \\ \geq &k \cdot \ln(p_k) \geq \frac{ \ln(2) }{ 2 } \cdot p_k \tag{7}\label{7} \\ \end{align} $$

Then, if we bring out the exponent in the logarithm, expand out the multiplication and division, and then isolate the \( p_k \) on the right, we get

$$ \begin{align} &\frac{4}{\ln(2)} \cdot [ k \cdot ( \ln(k) + \ln(2) - \ln( \ln(2) ) ) ] \\ &\geq p_k \tag{8}\label{8} \\ \end{align} $$

Now let’s work on the left side of equation (8). When you multiply out

\[ \frac{4}{\ln(2)} [ \ln(2) - \ln( \ln(2) ) ] \]

you get something that is slightly less than \(3 \). Therefore we can replace equation (8) with

\[ \frac{4}{\ln(2)} k \ln(k) + 3 \geq p_k \tag{9}\label{9} \]

and since

\[ \frac{4}{\ln(2) } < 6 \]

we can conclude

\[ 6 \cdot k \ln(k) + 3 \geq p_k \tag{10}\label{10}\]

When \( k > e \), \( \ln(k) > 1\), so whenever \( k \) is sufficiently large, making the \(6\) larger does more to increase the value of the left side of the inequality than adding the 3. If we increase the \(6\) to a \(10\), and then make sure that \(k\) is large enough, say \(10\) also, we have done more to increase the left hand side than adding the 3. Here’s what happens when we do that:

$$\begin{align} 6 \cdot 10 \cdot \ln(10) + 3 \approx 141.1551 … \\ 10 \cdot 10 \cdot \ln(10) + 0 \approx 230.2585… \end{align}$$

Using this, we see that when \(k \geq 10 \)

\[ 10 \cdot k \ln(k) \geq p_k \]

Now we’re almost done! Because that gives us

\[ \frac{1}{10} \cdot \frac{1}{k \cdot \ln(k) } \leq \frac{1}{p_k} \]

which gives us:

\[ \frac{1}{10} \cdot \sum\limits_{k = 10}^N \frac{1}{k \cdot \ln(k) } \leq \sum\limits_{k = 10}^N \frac{1}{p_k} \]

and we showed by lemma (a) that the left side goes to infinity as \(N\) goes to infinity.

QED