Zassenhaus Lemma and the Jordan Holder Theorem

We’re going to prove some results that will help us further get a feeling for the possible structure of groups. We’re going to start out by proving Zassenhaus’ Lemma. At least that will be our first significant result for this entry. Before we can do that, though, we’ll have to establish several smaller lemmas to support the proof. The first of these is mostly a useful observation. Finally, we’ll end the entry with a proof of the Jordan Holder Theorem.
Mini-lemma (products of intersections)
Let \(W\), \(X\), \(Y\), and \(Z\) be subsets of a group, then
$$ \begin{align} &(W \cap X) (Y \cap Z) = \\ &WY \cap WZ \cap XY \cap XZ \end{align} $$
Proof
Notice that \(WY \cap WZ = W(Y \cap Z) \). To see that, consider \(g_1g_2 \in W(Y \cap Z) \), then \( g_1 \in W\), while \( g_2\) is in both \(Y\) and \(Z\). Similarly, \(XY \cap XZ = X(Y \cap Z) \). Combining those two results and then applying the same logic to the \(W\) and \(X\) before the \( (Y \cap Z)\) gives our result.
QED
We’re going to state Zassenhaus’ Lemma, and then prove it later on in the entry. By doing this, we’ll give better motivation for the next few lemmas.
Theorem (Zassenhaus’ Lemma)
Let \(A\), and \(B\) be two subgroups of a group. Let \( a \triangleleft A\) and \(b \triangleleft B\) be normal subgroups of the two groups. Then $$ \begin{align} a(A \cap b) &\triangleleft a(A \cap B) \tag{1}\label{1} \\ b(a \cap B) &\triangleleft b(A \cap B) \tag{2}\label{2} \\ \frac{a(A \cap B)}{a(A \cap b)} &\cong \frac{b(A \cap B)}{b(a \cap B)} \tag{3}\label{3} \\ \end{align} $$
It can be visualized nicely with this lattice
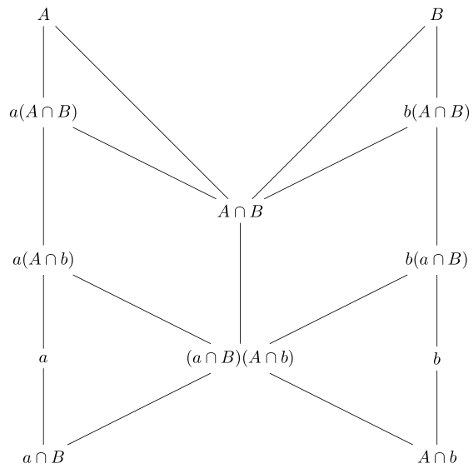
The very first thing you will want to notice is that since \( a \triangleleft A\), we have \(a \triangleleft (A \cap B) \), and \(a \triangleleft (A \cap b) \), so the set products along the left side are subgroups. Similarly, the set products along the right side of the lattice are also subgroups (we proved this here in Partial Orders, Lattices, and some Subgroups).
Because the lattice looks a bit like a butterfly (if you stand back and squint a bit), it is sometimes referred to as the Butterfly Lemma. We’ll prove equation (3) by showing that both sides are isomorphic to
\[ \frac{A \cap B}{(a \cap B)(A \cap b)} \tag{4}\label{4}\]
However, before we get to that, we’re going to rewrite the group products using our mini-lemma above. $$ \begin{align} a(A \cap B) &= A \cap aB \tag{5}\label{5} \\ a(A \cap b) &= A \cap ab \tag{6}\label{6} \\ b(A \cap B) &= bA \cap B \tag{7}\label{7} \\ b(a \cap B) &= ba \cap B \tag{8}\label{8} \\ \end{align} $$
All of these follow immediately from the mini-lemma and the fact that \(aA = A \) ( because \(a \subseteq A \)) and \(bB = B\), etc…
Next we focus on set product \( (A \cap b)(a \cap B) \). It contains both groups \( A \cap b \) and \(a \cap B \) as subsets. Thus, if it is a group, it is their join (we defined join in the previous entry Partial Orders, Lattices, and some Subgroups. It is simply the smallest subgroup of \(G\) which contains both \( A \cap b \) and \( a \cap B \) as subgroups). Again, using the mini-lemma at the top of this entry,
$$ \begin{align} &(a \cap B)(A \cap b) = \\ &A \cap B \cap ab \tag{9}\label{9} \end{align} $$
This equation follows because expanding the product out, we get \( aA \cap ab \cap BA \cap Bb \). We see that the first and last terms are \(A\) and \(B\), while the set \(BA\) contains both \(A\) and \(B\), so it contributes nothing to the overall intersection (i.e. it does nothing to further reduce the end result of the intersections). This doesn’t prove that it is a subgroup, though. However, that’s easy to establish, as it is the intersection of the subgroup \(B\) and \(A \cap ab = a(A \cap b) \), which are both subgroups.
Next we’re going to show that $$ \begin{align} &a(A \cap b ) \vee (A \cap B) \\ &= a(A \cap B) \end{align} $$ We’ve written it into the subgroup lattice above, but just because we drew it that way, doesn’t mean it’s actually so. Notice by equations (5) and (6), we need to show that
$$ \begin{align} &(A \cap ab) \vee (A \cap B)\\ &= A \cap aB \end{align} $$
Notice also that since the set product of the two subgroups contains both subgroups, that if it is a group, then it contains their join (this is the exact same reasoning we used above with the previous set product). Since their set product must also be a subset of their join, it would then have to be equal to their join.
By the lemma at the top of the page,
$$ \begin{align} &(A \cap ab) (A \cap B) = \\ &AA \cap AB \cap abA \cap abB \\ \end{align} $$
We’ve mentioned before that \(AA = A\). Notice that both \(AB \) and \(abA\) are larger sets than \(A\), so we can ignore both of their contributions to the intersection. And finally, since \(bB = B\), we are left with \(A \cap aB\), which is the result we were after.
$$ \begin{align} &a(A \cap b ) \vee (A \cap B) \\ &= a(A \cap B) \tag{10}\label{10} \\ \end{align} $$
Before we start proving (1) and (2), let’s prove another quick lemma.
Lemma (normal through alpha inverse of alpha)
Let \(G\) be a group, \(N \triangleleft G\), \(H \leq G\), \( M \triangleleft H\), then if \( \alpha : G \rightarrow G / N \) is the natural homomorphism sending \(g \in G\) to \( gN \in G/N \), then
\[ \alpha^{-1} \circ \alpha (M) \triangleleft \alpha^{-1} \circ \alpha (H) \tag{11} \label{11} \]
Proof
Let \(h N\) be an arbitrary coset of \(G\) in \( \alpha^{-1} \circ \alpha(H) \) (to be clear, since it belongs to \( \alpha^{-1} \circ \alpha (H)\), we are viewing it as a subset of G, instead of as an element of \(G/N\). We can switch between the two ways of viewing it, though). Let \( m_1N \subseteq \alpha^{-1} \circ \alpha(M) \) (this might be even less clear. It is a subset of \(MN\), corresponding to the coset of a single element of \(M\).). Now consider the set products, \( (hN)^{-1} (m_1N)(hN) \). Since \( N \triangleleft G\), this is equal to \( (h^{-1}N ) (m_1N) (hN) \), which is equal to the coset \( (h^{-1}m_1h) N \) of \(N\) in \(G / N\). Since \(M \triangleleft H\), this is equal to \( m_2 N\), for some \( m_2 \in M\). Therefore, for any \( h \in HN = \alpha^{-1} \circ \alpha (H) \), we must have \( h^{-1} MN h \subseteq MN \), and so they must be equal, as cosets.
QED
Mini-lemma (2)
\(B \leq G\), \(A \leq G\), and \(b \triangleleft B\) implies that \( (b \cap A) \triangleleft (B \cap A)\).
Proof
The notation is starting to get a little bit cumbersome, but bear with it, please. Let \(b_1\) be an element of \(B \cap A\). Then, since \(b \triangleleft B\), we have \( b_1^{-1}(b \cap A) b_1 \subseteq b \). What this is saying is that the element \(b_1\) conjugating the subgroup \((b \cap A)\) is equal to a subset of \(b\). This happens because \(b_1 \in B\), and \( (b \cap A) \subseteq b\). And when \(b_1\) conjugates any element of \(b\), the result must lie in \(b\).
Notice also that since \(b_1 \in (b \cap A) \) that \( b^{-1} (b \cap A )b_1 \subseteq A \). This is because all of the operations involved in that conjugation are among elements of \(A\). Combining these two facts gives us \( b_1^{-1}(b \cap A) b_1 \leq (b \cap A \). Therefore, since it is a coset of \(b \cap A\), the two sets must be equal. QED.
Now we’re all set up to combine the previous two lemmas to show that equation (1) above in Zassenhaus’ lemma is true. This follows immediately from recognizing that \( \alpha^{-1} \circ \alpha(A \cap b) = a(A \cap b) \), and that \( \alpha^{-1} \circ \alpha (A \cap B) = a(A \cap B )\).
In (Part 2) Counting Orbits, Sylow’s Theorems, etc… we established the basic isomorphism result that \( H \leq N_{G}(N) \) implies that \( HN / N \cong H / (H \cap N) \). We’re going to apply that by setting \( (A \cap B) = H \) and \( a(A \cap b) = A \cap ab = N \). First we need to show that \( (A \cap B \leq N_{G}( A \cap ab) \).
Lemma (3)
\(G\) is a group, \(A\), \(B\), are subgroups. Let \(a \triangleleft A \), and \(b \triangleleft B\), then \( (A \cap B) \leq N_{G}(A \cap ab) \).
Proof
Let \(a_1 \in (A \cap B)\) be equal to \(b_1 \in (A \cap B) \). We write it this way to emphasize that it is both an element of \(A\) and of \(B\). Let \(a_2b_2 \in ab\). That is, \(a_2 \in a\) and \(b_2 \in b\). This means that \(a_2\) is an element of the subgroup \(a\), and \(b_2\) is an element of the subgroup \(b\). Notice that
$$ \begin{align} &a_1^{-1}(a_2b_2)a_1 = \\ &a_1^{-1}a_2(a_1 a_1^{-1}) b_2 a_1 \\ \end{align} $$
We simply inserted an additional \(a_1 a_1^{-1} \) into the expression, which is nothing more than adding the identity into the product. Further notice that since \(a_1 = b_1\) we can rewrite this as
\[ (a_1^{-1} a_2 a_1) (b_1^{-1} b_2 b_1 ) \]
Notice how since \(a \triangleleft A \), the expression in the left pair of parentheses is equal to an element of \(a\), and similarly the expression in the right pair of parentheses is equal to an element of \(b\). Thus it is equal to an element of \(ab\).
It’s even easier to see that the product is an element of \(A\), since all the terms in these expressions are elements of \(A\).
QED
Finally (!) we are all set to apply the isomorphism theorem.
Let
$$ \begin{align} H &= (A \cap B) \tag{12}\label{12} \\ & \text{and} \\ N &= a(A \cap b) \\ &= A \cap ab \tag{13}\label{13} \\ \end{align} $$
Then by equation (10) above \(HN = H \vee N = a(A \cap B) \), and clearly \( H \cap N = (A \cap B) \cap (A \cap ab)\) which is equal to \(A \cap B \cap ab \), which, according to equation (9) is equal to \( (a \cap B)(A \cap b) \). Ergo, \(HN / N \cong H / (H \cap N) \) gives us
\[ \frac{a(A \cap B)}{a(A \cap b)} \cong \frac{A \cap B}{(a \cap B)(A \cap b)} \] A very similar argument, but with the \(A\)’s and \(B\)’s swapped, gives us
\[ \frac{b(A \cap B)}{b(a \cap B)} \cong \frac{A \cap B}{(a \cap B)(A \cap b)} \]
Combining the above two results proves part 3 of Zassenhaus’ Lemma. We’ve already established parts 1 and 2.
QED (Zassenhaus’ Lemma)
The final line of the above proof relied on the fact that isomorphism \( \cong\) is an equivalence relation. It is an equivalence relation. You can see this by observing that the composition of two isomorphisms will preserve operations, and will also be a bijection, since it is the composition of two bijections.
\[ \phi_1 : H_1 \rightarrow H_2 \] \[ \phi_2: H_2 \rightarrow H_3 \]
Then \( \phi_2 \circ \phi_1 H_1 \rightarrow H_3 \). Now we’re going to see what happens when we have a whole flock of butterflies.
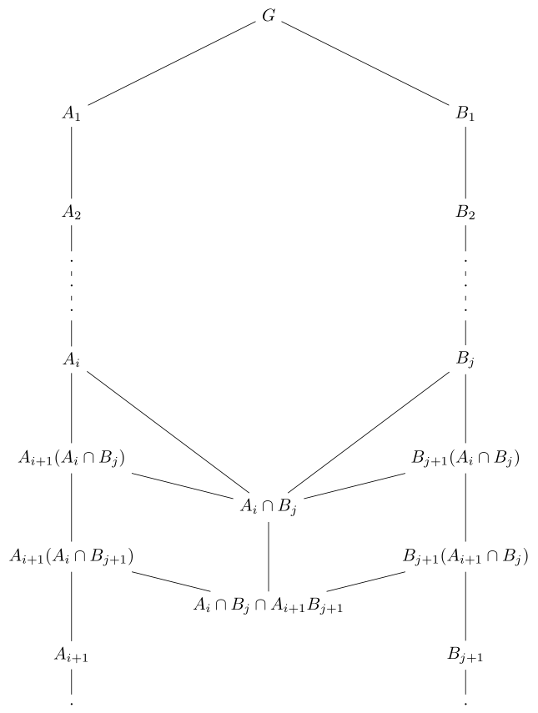
We’re going to draw your attention to a few facts about this. Notice first that if \(B_j = \{e\} \), then \(A_{i+1}(A_i \cap B_j) = A_{i+1} \). Second, if we consider \(G = A_0 = B_0\), then the set of \(A_{i+1}(A_i \cap B_j) \)’s contains every \(A_i\), when we index from \(i =0\), instead of \(i = 1\). Similarly, the set of all \(B_{j+1}(A_i \cap B_{j+1}) \) contains every \(B_j\), when we index from \(j = 0\), instead of \(j = 1\). Notice that this works even if \(A_1 = G\), or \(B_1 = G\).
To recap this,
$$ \begin{align} &\{ A_{i+1}(A_i \cap B_j) | 0 \leq i, 0 \leq j \} \\ &\supseteq \{A_i | i \geq 1 \} \\ \\ &\text{and,} \\ \\ &\{ B_{j+1}(A_i \cap B_j) | 0 \leq i, 0 \leq j \} \\ &\supseteq \{B_j | j \geq 1 \}\\ \end{align} $$
Furthermore, Zassenhaus’ lemma tells us that
\[ \begin{align} &\frac{A_{i+1}(A_i \cap B_j)}{A_{i+1}(A_i \cap B_{j+1})} \\ \cong &\frac{B_{j+1}(A_i \cap B_j)}{B_{j+1}(A_{i+1} \cap B_j)} \end{align} \]
Combining these facts tells us that if we have any two sets of factor groups (as long as they both contain the trivial subgroup \( \{e \} \) !), then we can construct a third set of factor groups which contains factor groups which are isomorphic to every factor group in the first two sets.
In case it’s not perfectly clear what we’re saying, let
$$ \begin{align} \mathcal{A} &:= \\ &\{A_1, A_2, … , A_m = \{e \}\} \\ \\ \mathcal{B} &:= \\ &\{ B_1, B_2, … , B_n = \{e\}\} \\ \end{align} $$
Where \( A_{i} \triangleright A_{i+1}\) and \(B_j \triangleright B_{j+1} \). Then let
$$ \begin{align} &\mathcal{A}_{/} := \\ &\{ A_1/A_2, A_2/A_3, … A_{m-1}/A_{m} \} \\ \end{align} $$
and
$$ \begin{align} &\mathcal{B}_{/} := \\ &\{ B_1/B_2, B_2/B_3, … B_{n-1}/B_{n} \} \\ \end{align} $$
Then if we let (remember, we’re setting \(A_0 = G = B_0\))
$$ \begin{align} \mathcal{C}^{A} &:= \{ A_1(A_0 \cap B_0) , A_1(A_0 \cap B_1), \\ &… , A_1(A_0 \cap B_n) = A_1, \\ &… , A_m(A_{m-1} \cap B_n) = \{e\}\} \\ \\ &\text{and} \\ \\ \mathcal{C}^{B} &:= \{ B_1(A_0 \cap B_0) , B_1(A_1 \cap B_0), \\ &… , B_1(A_m \cap B_0) = B_1, \\ &… , B_n(A_{m} \cap B_{n-1}) = \{e\}\} \\ \end{align} $$
They both have \(m \cdot n\) subgroups in them. Furthermore, \( \mathcal{C}^{A}_{/} \) and \( \mathcal{C}^{B}_{/} \) both have \(m \cdot n - 1\) factor groups, and every factor group in one set is isomorphic to a factor group in the other set. This result was originally proved by a mathematician named Shreier.
We have just a few more things to get through, and then we’re finished with this entry (Yay!).
Lemma (another isomorphism theorem)
Let \(G\) be a group, \(M \triangleleft G\), \(N \triangleleft G\), and \( N \triangleleft M\), then \[ G /M \cong \frac{G / N}{N / M} \tag{14}\label{14}\]
Proof
Let \( \alpha : G /N \rightarrow G/M \) be such that \( \alpha(gN) = gM \). Then \( \alpha(gN) = eM \), if and only if \(gN \subseteq M \). Therefore, \( Ker(\alpha) = \{ mN | m \in M \} \). I.e. \( M / N \).
QED
Corollary 1
If \(G/N \) is a simple group (i.e. it has no normal subgroups), then \( G \triangleright M \triangleright N \) implies either \( M = G\), or \(M = N\).
Proof
By equation (14), we see that if \(M\) isn’t either \(G\), or \(N\), then \(G/N\) has a non-trivial normal subgroup, which cannot happen.
QED
Corollary (Jordan - Holder Theorem)
Let \(G\) be a group. Let \( \mathcal{A} = \{ A_i\}^{n}_{i = 1}\) be a set of subgroups, such that \(A_1 = G\), \(A_n = \{e\}\), and \(A_i \triangleright A_{i+1}\). Furthermore, suppose that \(A_i / A_{i+1} \) is simple and that \(A_i \neq A_{i+1} \) for any \(i\). Let \( \mathcal{B} \) be another such set of subgroups. Then,
\( \mathcal{A} \) and \(\mathcal{B} \) have exactly the same size.
\( \mathcal{A}_{/} \) and \( \mathcal{B}_{/} \), the sets of factor groups of \( \mathcal{A} \) and \(\mathcal{B} \) respectively, have the same size. Each element of one is isomorphic to an element of the other. Moreover, there is a permutation mapping each element of \( \mathcal{A}_{/} \) to an isomorphic element of \( \mathcal{B}_{/} \).
Proof
Combine the previous corollary with Shreier’s theorem above.
QED
